Планирование эксперимента и анализ данных
Опубликовано 09.12.2019 в ChSU
Приветствую всех заинтересованных!
Данный раздел посвящен основам планирования эксперимента и анализу полученных данных. Это является основной любой научной и аналитической работы. При этом я не вижу больших различий в том, какая это будет наука или дисциплина. По сути мы проводим эксперименты и обрабатываем данные постоянно в нашей жизни. Так что постараюсь сделать этот курс максимально полезным и осмысленным вне зависимости от области применения. Ведь все мы в той или иной мере являемся учеными и инженерами и в обычной жизни (вопрос в том: хорошими или плохими?). Мы решаем различные оптимизационные задачи (например, как получать бОльшую зарплату), накапливаем данные через наблюдения и строим выводы, опираясь на собственный опыт.
Целью курса является формирование общих теоретических и практических представлений о том, что такое наука, данные и эксперимент.
Основные задачи:
- Показать терминологию и логику построения экспериментов в науке.
- Описать особенности проведения эксперимента с точки зрения исследуемых факторов.
- Определить эффективные пути проведения эксперимента и получения информации с целью оптимизации отклика системы.
- Дать введение в статистику и обработку результатов.
- Познакомить с построением линейных регрессионных моделей со статистической точки зрения.
- Рассмотреть и решить некоторые примеры и задачи по теме курса.
Многие задачи и определения взяты с прекрасных курсов coursera.org и stepic.org (подробнее в списке литературы), а также из различных учебников и пособий по аналитической химии. Категорически рекомендую вам эти платформы дистанционного обучения.
Весь представленный здесь материал исследован, структурирован и переработан исходя из собственного опыта работы и отражает мой субъективный взгляд на вещи.
0. Оглавление
- Введение. Наука и научный подход
- Эксперимент. Система и факторы
- Введение и терминология
- Анализ двухфакторного эксперимента
- Построение прогнозов
- Взаимодействие между факторами
- Трехфакторный эксперимент
- Построение модели методом наименьших квадратов (МНК) для 2 факторного эксперимента
- Анализ факторного эксперимента с использованием RStudio
- Сокращение затрат на эксперименты
- Построение карты эксперимента
- Заключение
- Вопросы по разделу
- Сравнительные эксперименты. Статистическая практика
- Построение точных моделей. Аналитическая практика
1. Введение. Наука и научный подход
Итак, наука и научный подход — что это такое?
Наука (от лат. scientia — знания) — системное представление о строении и организации знаний (информации) о вселенной с возможностью проверки и предсказания.
Вообще, как известно из древнегреческой философии, для изучения окружающего мира человеку доступно лишь две возможности: наблюдение и эксперимент. Данное утверждение можно принять за аксиому (по крайней мере я не встречал противоречий и в современном мире).
При этом научную деятельность можно охарактеризовать следующим образом - это сбор данных через наблюдения и эксперименты. Их постоянное обновление, систематизация и анализ. Следствием всего этого является получение (синтез) новых знаний и законов нашего мира.
Другими словами: на основе данных, мы создаем теории и гипотезы, которые подтверждаются/опровергаются наблюдениями или экспериментами. Это и есть наука. Таким образом можно предположить следующий цикл научного познания (рис. 1, табл. 1).
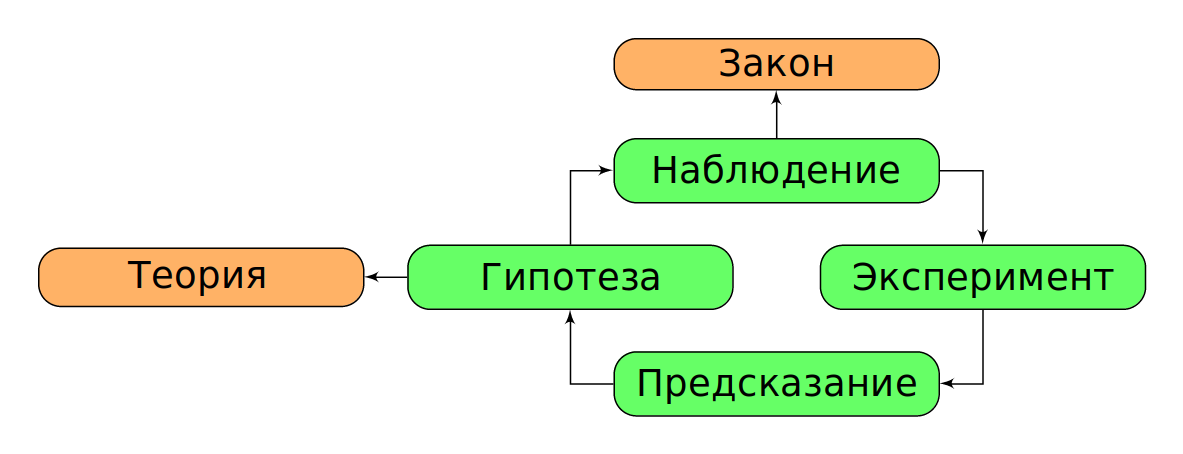
|
Рис. 1. Взаимосвязь научных понятий. |
Таблица 1. Термины научного познания
| применимо к единице или малому количеству | применимо ко всем случаем | |
|---|---|---|
| описывает что происходит | наблюдение | закон |
| объясняет почему явление происходит | гипотеза | теория |
Как правило в любой науке мы с вами будем работать над гипотезами и теориями, оперируя законами и наблюдениями (все на основе данных).
При этом не стоит забывать, что основным инструментом описания и классификации любого явления является математика. Для эффективной же работы в современном мире нам требуется еще один инструмент — программирование. Советую не забывать об этом и тогда ваша конкурентоспособность будет высокой.
Сам же эксперимент - это неотрывная частью науки и нашей жизни. Это запланированное наблюдение (проводимое с какой-либо целью). Все мы проводим эксперименты в повседневной жизни. Как сказал один преподаватель, если вы перестали экспериментировать - вы разочаровались в жизни. А это значит, что пора начать любое движение и снова экспериментировать.
Задача. Подумайте, какие эксперименты вы проводили в недавнее время? Что значит эксперимент для вас?
Вот хороший пример эксперимента. Допусти, мы выращиваем растение у себя перед монитором и поставили себе цель - оптимизировать его рост. В первую очередь, стоит проанализировать в чем выражается рост: длинна, количество листьев, вес и т.д.. Затем, нужно определить параметры, которые могут влиять на длину растения: количество воды для полива, частота полива, тип почвы, тип горшка для растения, тип удобрения, количество удобрения, свет, температура и т.д..
Таким образом, мы получили довольно много факторов, для которых нужно провести эксперименты, что бы узнать, какой фактор (или комбинация факторов) позволит нам добиться цели.
Примечание. Предлагаю запомнить последовательность: цель - факторы в которых выражается цель - влияющие на факторы параметры - эксперимент.
Из этого примера мы можем понять, с чем столкнемся дальше. Нам предстоит планировать и описывать эксперименты, а также обрабатывать данные и доказывать их правоту (представительность) с точки зрения статистики.
Для планирования эксперимента важно знать теорию соответствующей ему области знаний (в которой мы проводим этот эксперимент) и терминологию (что бы правильно ставить цели и определять параметры). Помимо этого, важно пользоваться обозначенным ранее научным циклом. А теперь, непосредственно к делу.
2. Эксперимент. Система и факторы
2.1 Введение и терминология
При проведении эксперимента, нашей целью является результат (outcome) - то, что мы хотим узнать/оптимизировать/представить в численном виде (т.е. то, что можно измерить). Синонимами результата являются реакция/оклик системы.
Факторы (factors, features) - изменяемые свойства, от которых предположительно зависит результат эксперимента (на них влияют соответствующие переменные (variables), но часто данные термины используют как синонимы).
Все эксперименты должны иметь хотя бы 1 изменяемый (и измеряемый) фактор. И чем больше факторов мы примем к рассмотрению, тем лучше (в общем случае).
Сами факторы делятся на:
- количественные (quantitative) - которые можно измерить и сравнить (упорядочить по возрастанию/убыванию);
- качественные (категориальные, номинативные, qualitative) - определяющие тип, но которые нельзя сравнить.
Иногда выделяют еще и ранговые факторы - определяющие тип, но которые можно сравнить (например, место в соревновании и т.п.). Но для анализа результатов в подавляющем случае используют только количественные или качественные величины. Ранговые величины используются при расчете различных статистических критериев.
Пример. Давайте рассмотрим классический пример построения эксперимента и обработки его результатов. Мы хотим увеличить прибыль магазина (\(= \text{доход} - \text{расходы}\)) и считаем, что на это будут влиять 2 фактора: освещенность помещения (можем выставить диммер освещения на 50% и 75%) и цена товара (допустим 7.79 $ или 8.49 $). Вот мы и столкнулись с двухфакторным экспериментом.
Отметим, что такой эксперимент нужно проводить 4 раза (например, каждый понедельник). Недостаточно просто менять по одному признаку (3 эксперимента), нужно добавить еще один - когда меняются оба признака сразу. Это увеличит количество полученной информации в 2 раза и позволит провести сравнение влияния обоих признаков на результат эксперимента. Дальше мы увидим почему это так.
При планировании эксперимента составляют специальную таблицу (табл. 2). Порядок записи данных в таблице называется стандартным порядком испытаний.
Таблица 2. Пример записи результатов эксперимента.
| No | real No | Dimmer, % | Price | Profit, $ |
|---|---|---|---|---|
| 1 | 3 | 50 | Low | 490 |
| 2 | 1 | 75 | Low | 570 |
| 3 | 4 | 50 | High | 370 |
| 4 | 2 | 75 | High | 450 |
Даже просто записав получившиеся результаты, мы можем начать их анализ. Например, эффект яркости света при низкой цене составляет 80 $ (разница между тусклым и ярким светом). Тот же эффект при высокой цене будет 80 $. Таким образом, мы наблюдаем увеличение прибыли на 80 $ от эффекта освещения. Можно заметить, что эффект сохраняется при разных уровнях цены.
Аналогично для эффекта цены: при слабой освещенности он составит 120 $, при ярком свете - тоже 120 $. Таким образом, при увеличении цены на товар, прибыль падает (для нашего случая).
Задача. Как Вы думаете, что могло пойти не так? Какие факторы мы не учли и что еще может оказывать влияние на прибыль? Является ли наш эксперимент воспроизводимым (получим ли мы те же результаты при изменении прочих факторов)?
Интересно, что для рассмотренного примера многие люди провели бы не 4, а 3 опыта в рамках эксперимента. В качестве первого опыта они выбрали бы слабую освещенность и низкую цену. Далее, они бы проведи второй опыт - увеличили яркость света (оставив неизменной цену). Затем, они вернулись бы к начальной точке и провели бы третий опыт, увеличив только цену.
Многие посчитают, что так и надо проводить эксперименты (потому что каждый раз вы меняете только один фактор). Вас учили этому в школе и университете. Менять только один параметр за раз. Но в общем случае так делать не надо!
Если вы ограничитесь тремя экспериментами, вы получите только одну оценку эффекта от освещенности и только одну оценку эффекта от цены. Однако, всего один дополнительный опыт при увеличении обоих факторов позволит нам оценить оба эффекта дважды. Мы получаем две оценки влияния освещенности и две оценки влияния цены на прибыль. Поэтому, добавив всего один дополнительный опыт, мы фактически удвоили количество полученной информации.
Во многих случаях, этот дополнительный опыт стоит затраченных усилий.
Примечание. Мы описали так называемый "полнофакторный" эксперимент (full factor experiment). при этом мы изменяли сразу оба параметра. Однако пример "фиксированного" подхода к эксперименту (когда мы меняем только один фактор при фиксированных прочих факторах) очень распространен в аналитической химии. В случае построения градуировочной прямой мы меняем обычно только одну переменную (аналитический сигнал) в фиксированных условиях и измеряем только один отклик (концентрацию). Как Вы думаете почему? Какую дополнительную экспериментальную работу необходимо сделать, прежде чем станет возможно зафиксировать остальные факторы?
Немного терминов для словарного запаса. Множество наших наблюдений за объектом есть процесс измерения. В свою очередь запись измерения в определенных величинах — это количественный анализ/измерение (сравнение с установленным стандартом, например, измерение линейкой). Таким образом, количественное измерение — записанный результат сравнения в определенной размерности. Качественный анализ — просто результат сравнения (больше или меньше, есть объект или нет, как правило без размерности). Иногда говорят о полуколичественном анализе, подразумевая не очень точный количественный анализ (но лучше, чем ничего).
2.1.1 Точность и воспроизводимость
Мы подошли к основным понятиям обработки результатов эксперимента: точность (прецизионность, accuracy) и воспроизводимость (precision). Лучше всего эти понятия объясняет аналогия с мишенями для стрельбы (рис. 2).
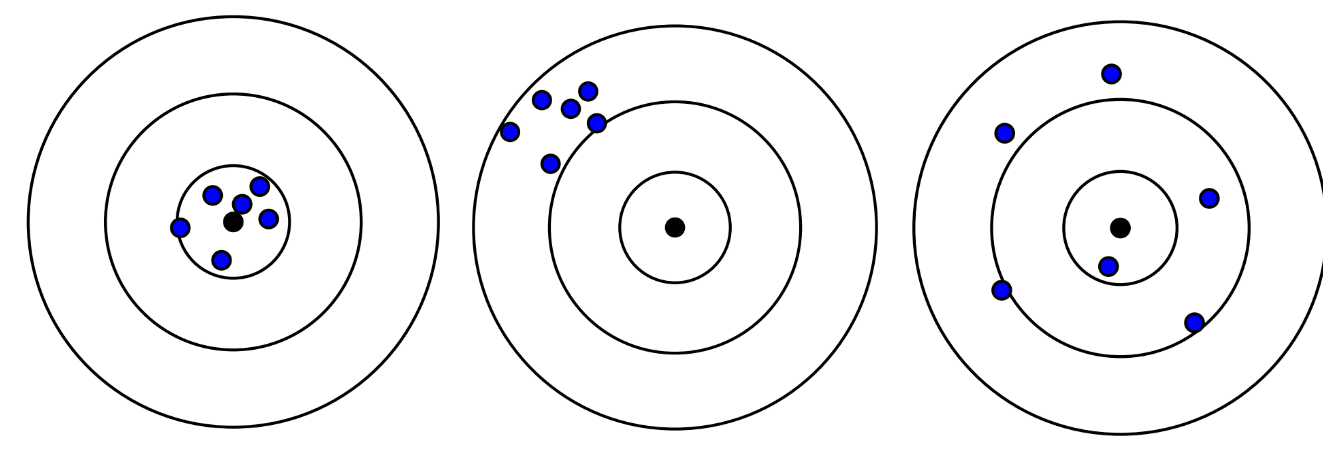
|
Рис. 2. Примеры с точностью и воспроизводимостью стрельбы. Точно и воспроизводимо, не точно и воспроизводимо и "точно" и не воспроизводимо (когда среднее значение не точных результатов оказывается случайно близким к истинному значению). |
Точность определяет близость полученного результата к абсолютному значению, а воспроизводимость — насколько близко от предыдущего полученного результата будет лежать следующее такое же измерение. Воспроизводимость и точность оцениваются с помощью очень важного и полезного инструмента — статистики (область математики).
Для оценки точности полученного результата мы можем использовать понятие абсолютной и относительной погрешности.
Абсолютная погрешность (absolute error): \(a = x_{true} − x_{our}\), где: \(x_{true}\) — истинное значение (как правило никогда не известно, поэтому за него обычно принимаем значение референтного метода анализа или среднее), \(x_{our}\) — полученное нами значение. Как можно заметить по формуле, абсолютная погрешность измеряется в тех же величинах что и само измерение.
Относительная погрешность (relative error): \(\Delta = \frac{x_{true} - x_{our}}{x_{true}}\). Относительная погрешность измеряется в процентах (на то она и относительная).
Воспроизводимость в свою очередь определяется немного сложнее и к ней мы вернемся в 3 части курса, посвященной статистической обработке результатов.
Стоит сказать, что существует всего 2 природы погрешности: случайная (random, обусловленная статистической природой измерений, всегда присутствует в нашем несовершенном мире) и систематическая (systematic), обусловленная действием какой-либо постоянной возмущающей силы, которую можно вычислить или учесть (например, гравитация, плохо откалиброванный прибор и т.д.).
Примечание. Распространенность "фиксированного" подход в аналитической химии вызвано тем, что он обеспечивает большую точность и достоверность полученных результатов. Однако, прежде чем выбрать наиболее значимый фактор и зафиксировать все остальные, необходимо тщательно изучить систему. Для этого и используется факторный эксперимент. Кроме того, факторный эксперимент доминирует в остальных областях знаний, включая химическую технологию.
2.1.2 Немного о правилах представления результата
Важным понятием любой естественной науки является понятие значащих цифр и правил округления. Помимо размерности, точности и воспроизводимости, нужно правильно оценить количество значащих цифр для полученных экспериментальных данных. Другими словами, нужно показать сколько цифр в полученном результате имеют реальное физическое обоснование (физический смысл). Прочие цифры нужно отбросить (точности мы не потеряем, но цифры станут достоверными).
Количество значащих цифр определяет погрешность эксперимента (и наоборот, результат измерения округляется до того же знака, что и абсолютная погрешность с одной значащей цифрой).
Пример. Если в ходе повторения эксперимента по измерению концентрации стандартного образца с установленной концентрацией в 100.0 моль/л мы получили значение 100.1, 99.8, 100.2, то средняя абсолютная погрешность составит \(\frac{\sum |x_i - 100|}{3} = \frac{0.1 + 0.2 + 0.2}{3} = 0.16666.. \approx 0.2\). Тогда средний результат измерения будет \(\frac{100.1 + 99.8 + 100.2}{3} = 100.0333... \approx 100.0\).
Обычно такой результат записывают в виде \(100.0 \pm 0.2\). Последняя цифра при такой записи получается как бы не точно определена и может принимать любое значение в пределах экспериментальной погрешности \(x \in [99.8; 100.2]\).
Значащие цифры очень полезны для естественных наук. Они позволяют упростить некоторые стадии эксперимента и сделать его более воспроизводимым, показать коллегам с какой точностью мы проводили исследования. Например, зная необходимую точность эксперимента и значащие цифры, можно рассчитать с какой точностью нужно взвешивать реактивы (если точность эксперимента ограничена 2 значащими цифрами, то взвешивать с 4 значащими цифрами нет смысла).
Далее мы приведем наборы правил для значащих цифр. Чтобы их понять и запомнить нужно мыслить категориями погрешности. Всегда помните, что последняя значащая цифра несет в себе неопределенность от абсолютной погрешности.
Для записи значащих цифр есть несколько правил.
- Каждая цифра, отличная от 0 - значащая (например, 237 — 3 значащих цифры, 129.7 - 4 значащие цифры).
- 0 перед не 0-ми числами — не значащий (0.0165 — 3 значащие цифры). В таком случае лучше применять "научную" запись числа: \(1.65 \cdot 10^{-1}\).
- 0 до десятичной точки — нельзя сказать наверняка, так ученый писать не должен (10 писать нельзя, записывать нужно как \(1.0 \cdot 10\). Однако к сожалению, такая запись очень часто встречалась в моей практике. Если вы встретили запись эксперимента в виде 3700 единиц, то скорее всего человек не знаком с практикой значащих цифр и просто округлил до целого. Лучше проанализировать эксперимент и установить количество значащих цифр (например, точность взвешивания или абсолютную погрешность).
- В остальных случаях 0 - значим (85.950 — 5 значащих цифр, 12.06 — 4 значащих цифры).
Примечание. Научная (экспоненциальная) запись числа всегда подразумевает одну цифру до десятичной точки и точное указание значащих цифр, например, \(1.650 \cdot 10^{-10}\) или \(2.740 \cdot 10^{5}\). Настоятельно рекомендую всегда пользоваться ею в экспериментальной практике.
Пример. Масса образца равна 0.1 г. Если взвешивание проводили на аналитических весах с погрешностью \(\pm 0.0001\) г, то правильное представление результата будет 0.1000 г или \(1.000 \cdot 10^{-1}\) г.
Также есть правила для арифметических действий со значащими цифрами, которые позволяют нам сохранить физический смысл величин при математических вычислениях в естественных науках.
- Сложение/вычитание — мыслите абсолютными категориями (важен порядок числа). Оставляют столько цифр после запятой, сколько их содержится в слагаемом с наименьшим числом десятичных знаков (т.е. точность лимитируется числом, имеющим наибольшую абсолютную недостоверность). Помните, что последняя цифра несет неопределенность, которая ограничивает все остальное, но при сложении ее влияние будет пропорционально ее порядку.
- Умножение/деление — мыслите относительными категориями (при умножении или делении недостоверность лимитирующего числа пропорционально переноситься на результат). Количество значащих цифр результата будет равно минимальному количеству значащих цифр участников (т.е. точность лимитируется числом, имеющим наибольшую относительную недостоверность). Если число значащих цифр одинаково, то лимитирует точность то, у которого мантисса меньше (абсолютная величина, равная всем выписанным подряд числам).
Пример. При \(0.0304 \times 5.43\) точность лимитирует первое (мантисса 1-ого 304, мантисса 2-ого 543). Это работает, поскольку относительная погрешность у меньшего числа будет больше.
- Логарифмирование - логарифмируемое число и мантисса (в случае логарифмирования - результат логарифма) содержат одинаковое количество значащих цифр.
Пример. Рассчитаем значение pH \(2.0 \cdot 10^{-3}\) М раствора HCl. Учтем, что основание логарифма и степени 10 в экспоненциальной записи числа - точные величины. Тогда результат:
$$ pH(2.0 \cdot 10^{-3}) = -lg(2.0 \cdot 10^{-3}) = -(lg(2.0) -3) = -(0.30 - 3) = 2.70 $$Обратите внимание, что за счет сложения с абсолютно точной величиной 3, точность конечного результата составила 3 значащих цифры (абсолютная погрешность измерения осталась прежней, а вот относительная погрешность уменьшилась).
- Возведение в степень - множественное умножение чисел, с одинаковым количеством значащих цифр и число значащих цифр результата будет таким же.
- Корень числа - можно представить как результат в абсолютной степени, т.е. множественное умножение результата, которое даст число, возводимое в корень. Таким образом число значащих цифр останется неизменным.
- Соблюдаем арифметический порядок действий как в математике.
- Во избежание накопления ошибки, округление результата делается только в конце всего вычисления. В промежуточных расчетах оставляем количество значащих цифр + 1. В конечном результате эта дополнительная цифра округляется.
Примечание. Приведенные правила вычислений со значащими цифрами есть не что иное, как приближение для погрешности результата. По этой причине чрезвычайно не желательно производить много расчетов для величин с погрешностями (особенно возведение в степень, взятие корня и логарифмирование) - чем больше таких операций, тем более не определен наш конечный результат в действительности. Правила обращения со значащими цифрами при математических операциях можно строго обосновать на основе закона распространения погрешностей (но делать так мы конечно же не будем).
Примечание. Результаты грави- и титриметрических определений в большинстве случаев записывают в виде чисел, содержащих 4 или 2 значащие цифры, что связано с погрешностью измерения массы веществ (например, \(\pm 0.0001\) г) и объемов (например, \(\pm 0.03\) мл) растворов. Но количество значащих цифр сильно зависит от исходной массы навески.
Примечание. Результат анализа и его погрешность должны содержать одинаковое число знаков после запятой (например, \(10.1 \pm 0.1\)).
Правила округления:
- округляем до количества значащих цифр (последняя несет в себе неопределенность);
- если отбрасываемая цифра больше пяти или меньше — округляем в соответствующую сторону;
- если отбрасываемая цифра 5 — округляем до ближайшего четного (если нужно округлить только одну цифру 5: \(10.5 \approx 10\), но это не так, если округляем 2 цифры \(10.51 \approx 11\));
- не округляем промежуточные вычисления или оставляем нужное количество значащих цифр + 1.
- всегда помните, что значащие цифры это показатель абсолютной погрешности измерения величины и работать с ними нужно соответственно.
Подводя итог еще раз рассмотрим зачем нам нужно всегда использовать значащие цифры, а не писать все что выводит нам калькулятор.
-
Являются достоверными и позволяют определять точность операций.
-
Можем определить лимитирующую стадию эксперимента (где наш эксперимент наименее точен и что в эксперименте стоит улучшить).
-
Показывают физический смысл округления чисел.
Пример. Необходимо рассчитать результат вычисления:
2.2 Анализ двухфакторного эксперимента
Я надеюсь, что смог показать вам как нужно записывать результаты экспериментов и убедил вас в значимости факторных экспериментов в нашей жизни. Время перейти к их изучению и анализу.
В качестве примера рассмотрим попкорн. Мы будем стараться оптимизировать количество лопнувших зерен. Этот эксперимент хорош тем, что вы можете повторить его у себя дома.
Примечание. Если что-то будет непонятно, то можете смело писать мне или посмотреть курс, где данный эксперимент разобран более подробно.
В самом эксперименте у нас будут 2 исследуемых фактора, которые принимают по 2 значения: А - время нагрева (160 и 200 с) и В - тип попкорна (желтый и белый). Можно легко посчитать, что число экспериментов будет 4.
Примечание. В общем случае для расчета количества экспериментов используют следующую формулу: \(f^v = 2^2 = 4\), где \(f\) - число факторов, а \(v\) - число значений, принимаемых фактором (согласно еще одной области математике - комбинаторике). В нашем случае мы всегда будем рассматривать одинаковое число уровней у факторов, считайте это своего рода требованием для подобных планов экспериментов.
Составим таблицу эксперимента (табл. 3). Обозначим низкое и высокое значение фактора как - и + соответственно (для категориального - не важно, выбираем любой). Тогда для А: - = 160, + = 200, для В: - = белый, + = желтый.
Примечание. Для получения информативных результатов важно:
- не использовать экстремальных значений для факторов (иначе на них оказывается множество влияний и они слишком сильно будут отличаться друг от друга, что увеличит погрешности);
- всегда проводить эксперименты в случайном порядке! Только так мы сможем избавиться от систематической погрешности и возникающих дополнительных связях между величинами.
Таблица 3. Результаты двухфакторного "попкорн-эксперимента".
| Standard order | Random order (real) | A - time * | B - corn | Results |
|---|---|---|---|---|
| 1 2 3 4 |
3 1 4 2 |
- + - + |
- - + + |
52 74 62 80 |
* используем стандартный подход: сначала все время изменяем 1-ый фактор, а 2-ой ставим ему в соответствие.
Итак, результаты получены. Само время проводить анализ. Начинать всегда лучше всего с визуализации (так уж устроено наше мышление). Визуализация факторного эксперимента называется кубической диаграммой (графиком/планом, cube plot). Она приведен на рис. 3.
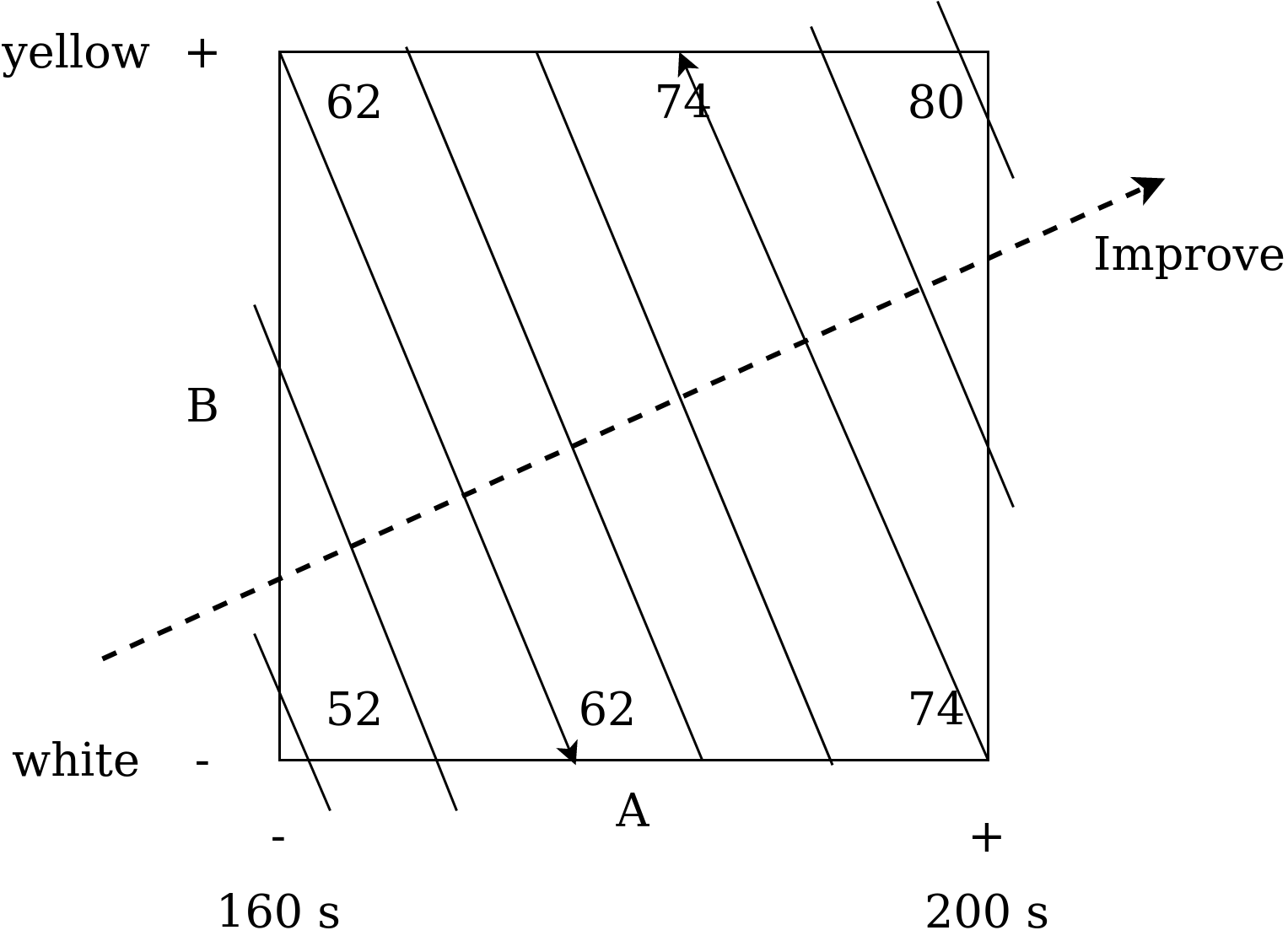
|
Рис. 3. Кубическая диаграмма 2-ух факторного эксперимента с попкорном. На диаграмме изображены изолинии. |
Эта диаграмма показывает эффект от каждого фактора в соответствующем углу квадрата или куба (2 или 3 факторные эксперименты).
Начнем с оценки эффекта от времени. При увеличении времени готовки для желтого попкорна, результат увеличивается с 62 до 80 лопнувших зерен (ЛЗ). Мы видим рост на 18 единиц. Для белого попкорна мы видим изменение с 52 до 74 ЛЗ, то есть рост на 22 единицы. Итак, в среднем мы видим увеличение на 20 единиц при увеличении продолжительности нагрева со 160 до 200 секунд.
Далее давайте оценим разницу между двумя типами попкорна. Зафиксируем время нагрева и посмотрим на эффект от перехода от белого к желтому попкорну: с 74 до 80 для 200 с и с 52 до 62 для 160 с. В среднем мы видим увеличение на 8 единиц при переходе от белого к желтому попкорну. Убедитесь, что ваша интерпретация соответствует кубической диаграмме. Эта визуализация очень важна для самопроверки результатов анализа.
Но помимо результатов, на кубической диаграмме отображены еще и контурные линии (contour plot, их еще называют изолиниями, isolines). Они обозначают область, в которой значение измеряемого признака остается постоянным (на 1 линии количество лопнувших зерен будет постоянным). Их рисуют начиная с любого угла кубической диаграммы, значение в котором не является максимальным или минимальным. Затем ищут это же значение на противоположенной стороне квадрата и проводят линию в соответствии с предполагаемым уровнем результата. Для проверки кривизны линии нужно рассчитать наше фиксированное значение для середины шкалы.
Затем рисуем вторую линию аналогично для значения в 74. Остальные рисуем параллельно полученным линиям.
Благодаря изолиниям можно быстро понять, куда начинать движение для оптимизации результата, т.е. по направлению к нашей цели. Например, если цель — максимизировать количество лопнувших зерен, то двигаться нужно перпендикулярно изолиниям в верхний правый угол. В данном случае это означает, что мы должны взять желтый попкорн и увеличить время приготовления (что вполне интуитивно понятно из кубической диаграммы).
Такой подход к оптимизации (с использованием изолиний) помогает нам определиться с метом проведения следующего эксперимента. Контурная диаграмма - это наш градиент (gradient, путь, по которому пройдут наши эксперименты для подтверждения/опровержения закона или теории).
Отмечу, что есть еще один способ визуализации - диаграмма взаимодействия (interaction plot) (рис. 4).
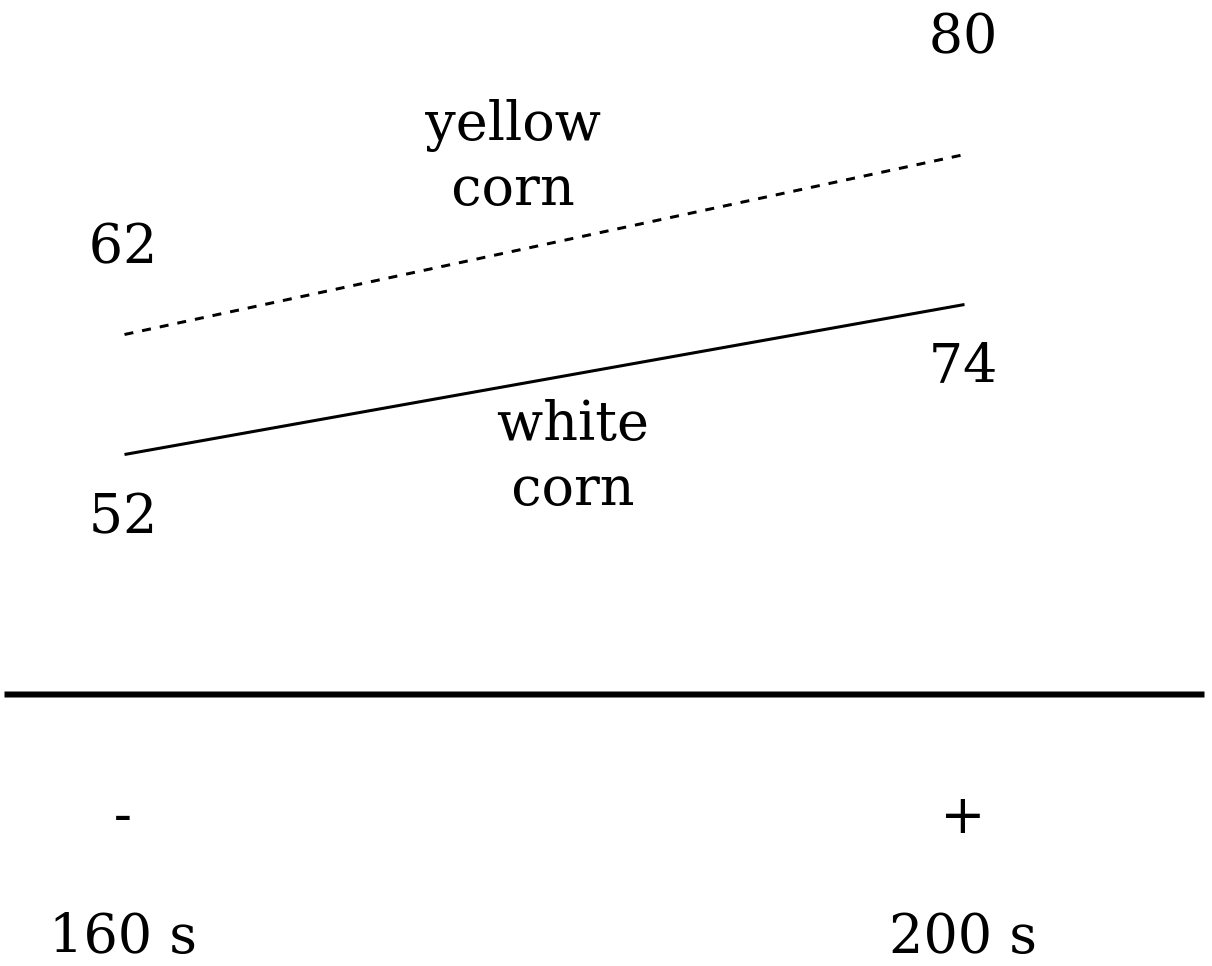
|
Рис. 4. Диаграмма взаимодействия для 2 факторного эксперимента с попкорном. |
Обратите внимание, что эти две линии практически параллельны, что означает, что в исследуемой системе практически отсутствует взаимодействие. Выбор переменной для диаграммы взаимодействия не играет большой роли и мы могли бы выбрать другую переменную для обозначения на горизонтальной оси.
Для всех описанных методов визуализации не требуется какое-либо программное обеспечение. Вы можете использовать эти методы визуализации как для числовых, так и для категориальных факторов. Все это демонстрирует явное преимущество такого подхода к эксперименту: мы можем быстро интерпретировать результаты, используя простые графические инструменты, элементарную математику и лист бумаги.
Тот факт, что все так просто, означает, что результатами будет легко поделиться с менеджерами или коллегами на работе.
2.3 Построение прогнозов
Мы рассмотрели пример планирования, проведения и анализа эксперимента. Но что это нам дает? Как мы можем представить и использовать полученные данные? Ответ - построить прогноз (модель, уравнение регрессии). В рамках нашего курса мы будем рассматривать только линейные модели (за небольшим исключением). Такие модели наиболее универсальные (любую гладкую и монотонную функцию можно представить как набор линейных отрезков).
В случае нашего "попкорн-эксперимента" (2-ух факторный эксперимент), полученная модель состоит из 3 частей:
где,
- \(a_0\) - базовый результат (intercept), который мы ожидаем увидеть при отсутствии влияния (когда закодированные значения факторов = 0). Этот коэффициент рассчитывается как среднее из 4 значений на кубической диаграмме (т.е. ее центр).
- \(a_1\) - коэффициент влияния фактора А (его закодированного значения), зависит от времени приготовления. Рассчитывается как средняя нормированная разница между высоким и низким значением фактора: \(a_1 = \frac{\frac{(80-62) + (74-52)}{2}}{2}\). Обратите внимание, нормировка подразумевает расчет коэффициента для единичного изменения фактора (т.е. с -1 до 0 или от 0 до +1), поэтому мы должны разделить усредненное значение на 2.
- \(a_2\) - коэффициент влияния фактора В, зависящий от типа зерен. Рассчитывается аналогично пункту 2.
Учитывая приведенное описание наша модель будет:
Задача. Проверьте корректность прогнозов этого уравнения для различных значений переменных A и B. Обращайте внимание на изолинии!
2.4 Взаимодействие между факторами
До сих пор мы рассматривали весьма идеальные случаи где нет взаимного влияния факторов друг на друга и на целевую переменную. Однако зачастую это не так.
Пример. Мы пытаемся отмыть руки и проводим 2-ух факторный эксперимент: есть/нет мыла и теплая/холодная вода. Можно заметить, что эффект теплой воды усилится при использовании мыла. И наоборот, эффект мыла усилится при использовании теплой воды. То есть "взаимодействие" говорит о том, что эффект одного фактора зависит от уровня другого фактора.
Кроме этого, эти взаимодействия обычно симметричны (не не всегда!). Т.е. нет разницы будем ли мыть руки в теплой воде с мылом или с мылом в теплой воде, результат будет одинаков.
Первым показателем наличия взаимосвязи является несимметричность линий на диаграмме взаимодействия или изогнутость изолинии на кубической диаграмме. Если вы наблюдаете такие эффекты, то это проявляется двухфакторное взаимодействие (когда поведение одной переменной сильно отличается в зависимости от уровня другой переменной).
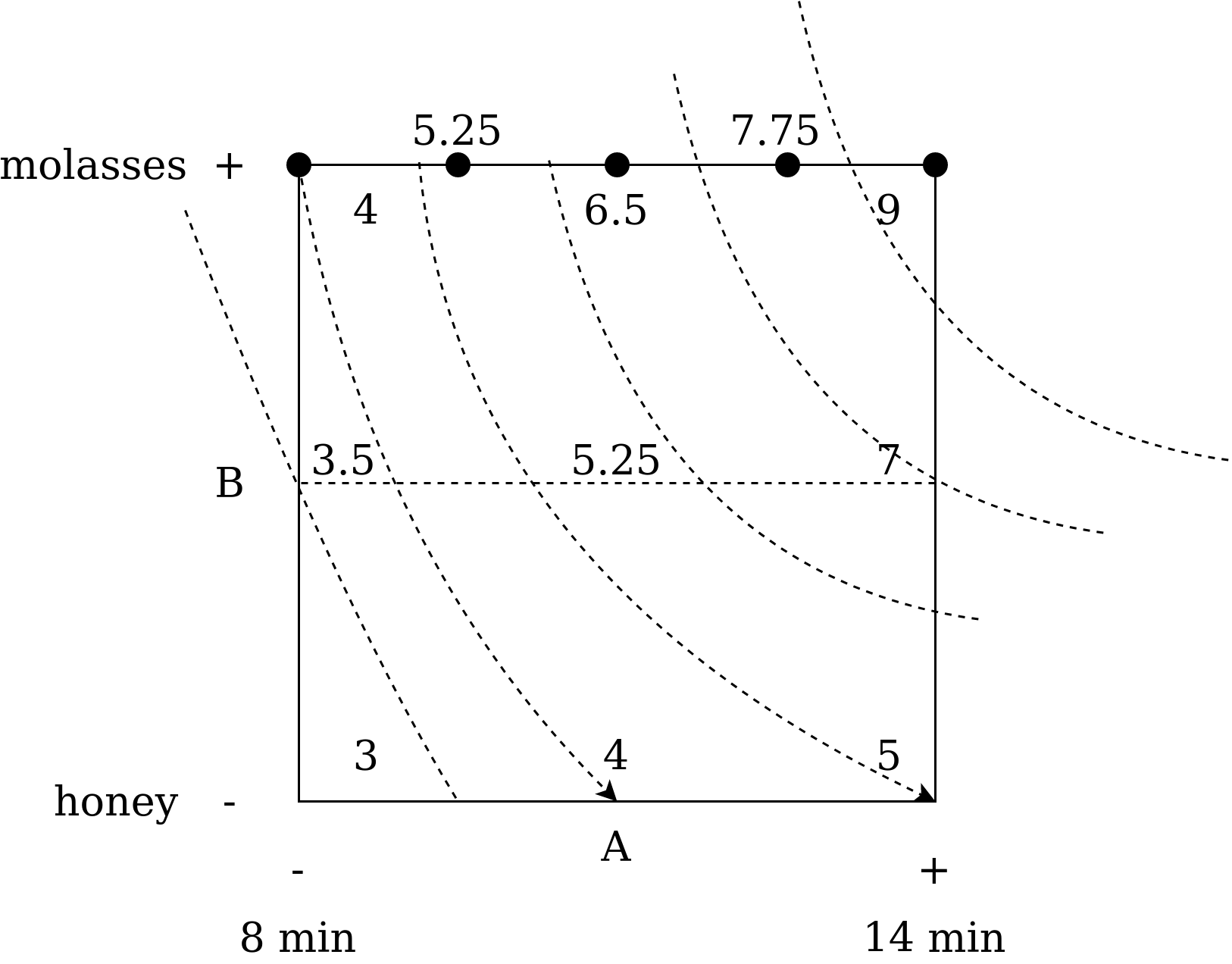
Рассмотрим эксперимент на рис. 5 и рассчитаем все коэффициенты. Эксперимент заключался в анализе влияния времени выпечки (фактор А) и типа подсластителя (фактор В) на вкус печенья (по шкале от 1 до 10).
|
Рис. 5. Кубическая диаграмма эксперимента со взаимодействием признаков. |
Обратите внимание, что изолинии уже не параллельные и изображать их нужно в изогнутом виде (еще раз напомню, на изолинии должно быть одинаковое значение результата). Для этого рекомендую провести вспомогательную линию по центру кубической диаграммы.
Выраженная не параллельность линий сигнализирует о наличии взаимного влияние факторов друг на друга. Строго говоря, при анализе эксперимента нужно всегда строить модель с учетом взаимного влияния и исключать его только если коэффициент перед этим фактором в модели очень мал. Рассчитаем получившуюся модель.
Для начала рассчитаем влияние каждого фактора на эксперимент в отдельности (без учета взаимного влияния, аналогично предыдущему примеру).
Затем, учтем фактор взаимного влияния, рассчитав изменения при одном фиксированном факторе (тип подсластителя). Тогда, математически, взаимодействие рассчитывается как усредненная разница при высоком и низком значении признака:
Это значение нормируется на единицу изменчивости фактора (уже классический прием).
Проверим симметричность влияния, зафиксировав другой фактор:
Таким образом влияние действительно симметрично и равнозначно. В итоге, наша модель запишется в виде:
Задача. Постройте диаграмму взаимодействия факторов и убедитесь в наличие взаимодействия. Проверьте точность предсказания нашей модели для краевых значений и различной времени готовки без учета взаимного влияния и с учетом взаимного влияния.
2.5 Трехфакторный эксперимент
После того, как мы освоили азы анализа результатов эксперимента, мы можем усложнить исходные условия.
Новый пример взят из учебника Бокса, Хантера и Хантера, которая называется "Статистика для экспериментаторов". В этом эксперименте проводится поиск оптимальной комбинации параметров для уменьшения количества загрязнителя в сточных водах очистных сооружений.
Рассматривается три фактора с 2 уровнями.
- Первый фактор — С (chemical), химическое соединение (два соединения P и Q).
- Следующий фактор - T (temperature), температура очистки воды (\(72^o F, $100^o F\)).
- Последний фактор - S (stirring speed), это скорость перемешивания (200 или 400 оборотов в минуту).
Тогда количество необходимых экспериментов составит:
где \(f\) - число факторов, а \(v\) - число значений, принимаемых фактором.
Результатом эксперимента будет количество загрязняющих веществ, измеренное в фунтах.
Используя стандартный порядок проведения эксперимента, составим таблицу эксперимента (табл. 4).
Таблица 4. Результаты трехфакторного эксперимента.
| Standard order | Random order (real) | C - chemical | T - time | S - stirring speed | Outcome |
|---|---|---|---|---|---|
| 1 2 3 4 5 6 7 8 |
6 2 5 3 7 1 8 4 |
- + - + - + - + |
- - + + - - + + |
- - - - + + + + |
5 30 6 33 4 3 5 4 |
Одно из преимуществ такой таблицы заключается в том, что мы можем быстро получить общее представление о влиянии фактора на результат. Например, оцените как изменяется количество загрязняющих веществ, когда мы меняем фактор химического соединения C? Уровень фактора меняется с низкого на высокий и мы видим ту же самую картину с количеством загрязняющих веществ. Посмотрите на эффект фактора S. Первые четыре эксперимента в среднем показали очень высокий уровень загрязнения, а последние четыре эксперимента — низкий уровень загрязнения.
Просто глядя на таблицу, мы можем сказать, что факторы C и S скорее всего важны для понимания полученных результатов.
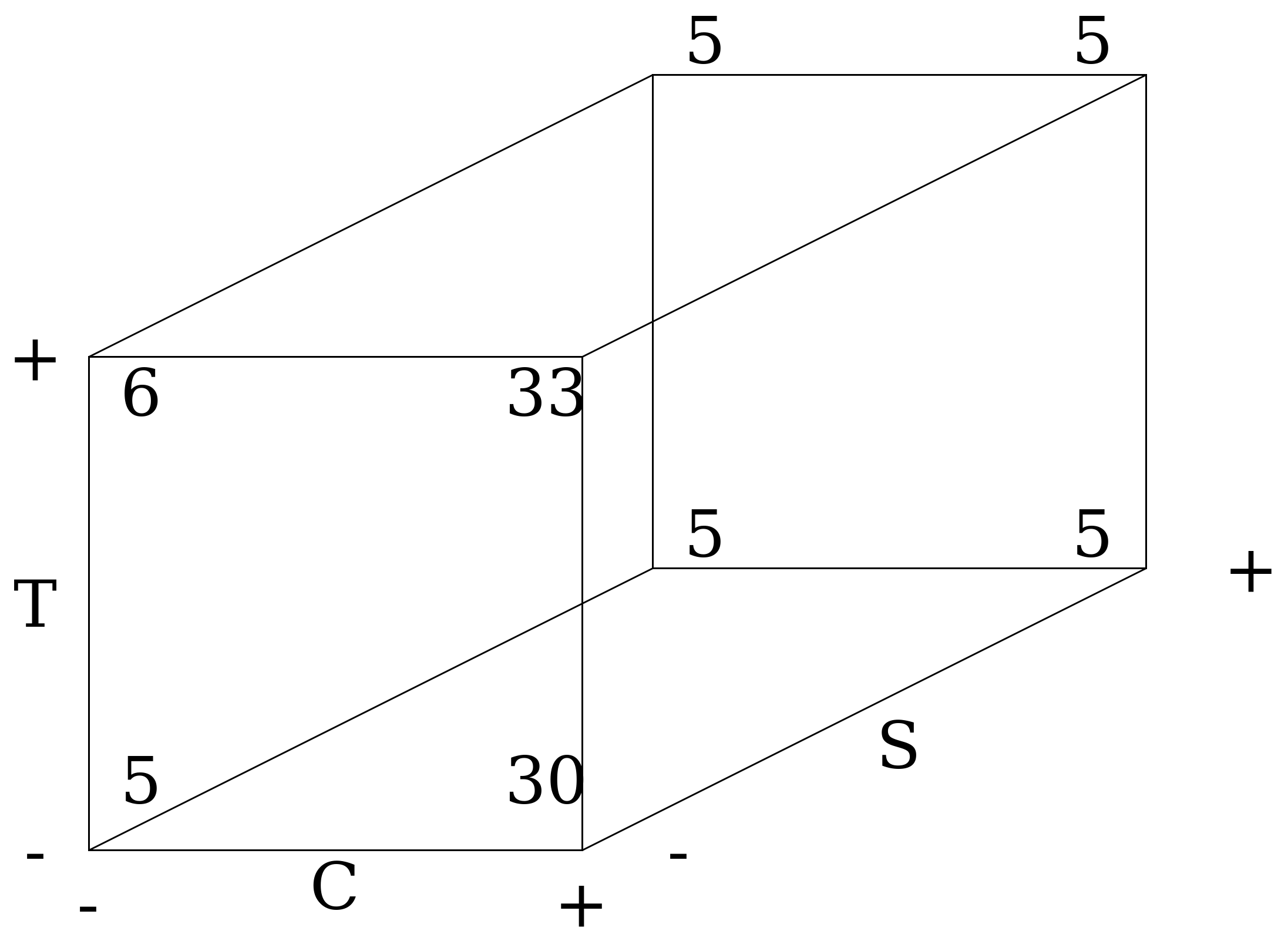
На основании таблицы эксперимента составим кубическую диаграмму (рис. 6.)
|
Рис. 6. Кубическая диаграмма трехфакторного эксперимента. |
Общий вывод. Согласно полученным результатам, нам нужно взять химикат Q, проводить очистку при низкой температуре и на высокой скорости перемешивания (400 оборотов в минуту).
Проанализируем основные эффекты и взаимодействия.
Начнем с первого фактора C (выбора между химическими соединениями P и Q, где Q — высокий уровень фактора). Из кубической диаграммы мы можем получить четыре оценки эффекта С (вдоль каждого из четырех горизонтальных ребер). При высокой температуре и высокой скорости перемешивания (т.е. высокий уровень T и высокий уровень S) эффект от этого фактора равен 4-5 фунтов загрязнения. При высокой температуре и низкой скорости: 33-6. При низкой температуре и высокой скорости (т.е. Т - и S +), эффект равен: 3-4. И, наконец, при низкой температуре и низкой скорости: 30 и 5.
Мы можем проанализировать полученную информацию с точки зрения каждого фактора и их возможного взаимодействия.
-
В ходе опытов, химическое соединение показало четыре результата. Среднее для этих четырех чисел равно \(\frac{50}{4} = 12.5\). Но что на самом деле означает полученное число 12.5? Как бы вы объяснили это значение своему менеджеру, который ничего не смыслит в статистике и экспериментах?
-
Значение в 12.5 говорит о том, что в среднем мы ожидаем увидеть увеличение количества загрязняющих веществ на 12.5 фунтов на тонну при переходе от химического соединения P к Q (хотя для модели используется коэффициент 6.25 - половина). Таким образом для категориальных признаков в модели мы пишем половину от эффекта (учитываем нормировку).
-
Еще одна вещь, на которую следует обратить внимание, это расхождение эффектов химиката при высоком и низком уровне перемешивания (S). Обратите внимание на огромную разницу, которая говорит о том, что существует явное взаимодействие между фактором C и фактором S.
-
-
Прежде чем мы перейдем к взаимодействиям, давайте рассмотрим температуру (T). Заметное влияние температуры на отклик системы в таблице отсутствует. Это же подтверждает рассчитанный коэффициент в модели = 1.5 единицы (или 0.75 при нормировании эффекта). Это действительно слабый эффект.
-
Наконец, рассмотрим эффект скорости перемешивания (S). Среднее для эффекта равно -14.5 (или -7.25 при нормировке). Другими словами, мы ожидаем среднее снижение количества загрязняющих веществ на 14.5 фунтов при переходе от низкой скорости перемешивания к высокой.
На этом этапе вам всегда надо делать паузу, чтобы убедиться, что полученные результаты имеют смысл. По горизонтальной оси мы видим, что переход от химиката P к Q увеличивает загрязнение (рис. 6). Поэтому значение 6.25 выглядит адекватно. Небольшое значение 0,75 для температуры также выглядит логично, потому что она действительно имеет очень слабый эффект. И, наконец, увеличение скорости перемешивания приводит к наиболее существенному снижению загрязнения: на 7.25 единиц.
Примечание. Всегда проверяйте полученные коэффициенты модели на разумность!
Как только мы закончили с интерпретацией факторов по отдельности, можно перейти к взаимодействиям. Ранее мы отметили, что эффект химиката сильно меняется при низкой скорости перемешивания. Однако на задней грани куба (при высоких скоростях перемешивания) эффект от выбора химиката практически равен нулю. Очевидно, что скорость перемешивания изменяет эффект от химического соединения. Таким образом мы наблюдаем взаимодействие между 2 факторами S и C. Для численной оценки воспользуемся уже знакомым нам приемом - добавим новый член в уравнение.
У нас есть две возможности его рассчитать, фиксируя разные уровни переменной:
- при высокой температуре;
- вторая — при низкой температуре.
Нет гарантии, что эффект будет симметричен, поэтому произведем оба расчета, а затем возьмем среднее (даже если эффект будет симметричен мы ничего не потеряем, а в противном случае - учтем оба влияния). А потом, как и всегда, нормируем на количество уровней признака (запишем половину).
Пока что, мы учли только взаимодействие между факторами С-S. По остальным двухфакторным взаимодействиям не наблюдается видимого значимого влияния (одна из возможных причин - температура слабо влияет на модель). На самом деле, есть еще и трехфакторное взаимодействие C-T-S. Но пытаться все это учесть в ручную весьма утомительно и велик шанс наделать при этом ошибок. Далее мы будем использовать для этого компьютер. Поэтому пока остановимся на полученных результатов и проанализируем их.
Общий анализ результатов. Основное заключение - при низких скоростях перемешивания химикат Q не эффективен, но при высоких оба химических соединения одинаково эффективны. Начиная с этого момента эксперименты становятся действительно мощным инструментом. Мы увидели, что самый низкий уровень загрязнений был при использовании химиката Q с высокой S и низкой T (найдите это значение на кубической диаграмме). Но что если, согласно требованиям правительства, загрязнение должно быть меньше 10? И при этом, допустим, химикат Q стоит вдвое дороже, чем P...
На самом деле мы сейчас мысленно оценили дополнительный результат — прибыль. Не забывайте, что прибыль (или расходы) часто играют важную роль во всех системах. Поэтому вы всегда должны иметь в виду экономическую составляющую каждого угла куба.
При этом мы убедились в малом эффекте температуры. И вот в чем вопрос: значит ли это, что рассматривать температуру в качестве фактора бессмысленно? И ответ - нет. Важно понимать, что даже незначительные эффекты представляют для нас важную информацию для изучения системы. Так, в нашем примере мы видим, что в диапазоне температур \([70; 100]^o F\) температура оказывает незначительное влияние на количество загрязняющих веществ. И это важно, потому что на основании этой информации инженер или оператор может подобрать наиболее экономически выгодные условия работы. И, опять-таки, все сводится к прибыли. Вполне вероятно, что работа при более низкой температуре позволит сэкономить энергию. А поскольку температура оказывает лишь незначительное влияние на систему в целом, мы не окажем существенного влияния на уровень загрязнения если решим работать при низкой температуре. И это отличный результат.
Задание. Постройте прогноз для любого случая из кубической диаграммы и проверьте его для модели без учета влияний и с учетом влияний. В какую сторону работают взаимодействия (увеличивают или уменьшают количество загрязняющих веществ)?
Задача. Как Вы думаете, почему химическое соединение Q оказывается менее эффективным при низкой скорости перемешивания, но при высокой работает очень хорошо?
2.6 Построение модели методом наименьших квадратов (МНК) для 2 факторного эксперимента
Дойдя до этого раздела, мы рассмотрели несколько важных примеров того, как нужно строить и анализировать эксперимент. Более того, мы научились рассчитывать модель, которая позволяет связать закодированные факторы с целевой переменной. Однако, коэффициенты для модели мы подбирали интуитивно, основываясь на вполне логичных представлениях об усреднении влияний признаков. Настало время более формального описания модели по результатам экспериментов.
Для построения математически обоснованной прогнозной модели мы воспользуемся наиболее распространенным подходом - методом наименьших квадратов (МНК). Мы еще затронем статистическое обоснование данного метода в 3 главе, а пока сосредоточимся на его общих особенностях и экспериментальном применении. В качестве примера, мы будем рассматривать наш "попкорн-эксперимент". Напомню, что линейная модель для двухфакторного эксперимента в общем случае выглядит как:
при этом \(x_A\) и \(x_B\) - кодированные переменные (через значения -1 и +1 мы кодируем реальные физические величины: для А - время, а для В - тип зерен).
В нашем случае проводилось 4 опыта, для каждого из которых должна быть справедлива предложенная модель. Тогда мы можем составить систему уравнений:
Таким образом, проведя эксперимент мы имеем 4 уравнения с 4 неизвестными, а значит - можем решить их!
Эти уравнения — линейные, поэтому система уравнений достаточно просто решается с использованием матричных методов. Не стоит пугаться, это просто более удобная форма записи и метод расчета. Давайте я покажу вам, как это сделать.
В матричной форме наши уравнения записываются следующим образом:
Значения в матрице \(4 \times 4\) состоят из кодированных переменных. Остальные 2 вектора (матрицы с одним столбцом или строкой данных) состоят из результатов опытов и неизвестных нам коэффициентов перед кодированными переменными.
В так называемом "аналитическом" виде (т.е. который имеет строгое математическое обоснование), такая матричная система имеет решение:
где \(b\) и \(y\) - векторы неизвестных коэффициентов и результатов эксперимента соответственно, а \(X\) - матрица кодированных переменных (\(X^T\) - транспонированная матрица, \((X)^{-1}\) - обратная матрица).
Примечание. Факторы не всегда должны быть кодированными (могут использоваться и обычные, "реальные" значения). Однако тогда мы можем столкнуться с рядом проблем (несбалансированность величин, неустойчивость решения и т.д.). Так что лучше всегда использовать кодированные значения (или хотя бы нормированные на среднее и дисперсию).
Найти описанное решение можно и в ручную (если использовать правила линейной алгебры). Однако лучше использовать компьютерные программы, которые очень эффективно решат за вас эти уравнения. Все, что нам нужно, это матрица \(X\) и вектор \(y\). И у нас есть все необходимое: матрица \(X\) получилась из таблицы эксперимента, а вектор \(y\) — это просто результаты четырех экспериментов.
Для компьютерных расчетов мы можем использовать ряд программ. Основные из них: MS Exel, R, Python и др. Как можно заметить, 2 из 3 перечисленных мною программ - языки программирования. Но не стоит их боятся. Например R - это очень распространенный и простой язык для статистики и анализа данных. Установить и использовать его довольно легко, а результат получается наглядным. С другой стороны современный Exel предоставляет весьма широкий набор функций работы с данными (в том числе работа с моделями и базами данных, pivot tables и т.д.). Помимо этого доступно множество платных и бесплатных программ для планирования эксперимента и анализа данных. Вы можете провести их поиск в интернете. Но в рамках нашего небольшого курса мы рассмотрим довольно простые примеры на R. Кроме того, более подробно работа с R рассмотрена в этом курсе с русскими субтитрами или другом, русскоязычном курсе.
2.7 Анализ факторного эксперимента с использованием RStudio
На предыдущих примерах вы научились выполнять необходимые расчеты и анализ результатов эксперимента в ручную. Однако при таком подходе наши возможности сильно ограничены, а риск ошибки очень высок. Время переходить на цифровые технологии! Для этого понадобится выбрать программное обеспечение для построения эксперимента и анализа данных. И на мой взгляд для этого отлично подходит язык программирования R и среда разработки RStudio.
Язык R и ПО для работы с ним бесплатны, имеют интуитивно понятный интерфейс, но самое главное, что R широко используется различными компаниями и исследователями. R настолько универсален, что вы можете использовать его даже в браузере. Можете воспользоваться этой возможностью, если не хотите устанавливать ПО или не можете им воспользоваться (например, потому что пользуетесь рабочим компьютером). Если все же Вы настроены серьезно и хотите работать на своем компьютере, то вам потребуется загрузить две программы: сам R и RStudio. В первом случае нужно будет выбрать место скачивания, наиболее быстрое или близкое к вам (Россия или Германия). Установите оба пакета программного обеспечения на компьютер и запустите RStudio (она уже сама будет запускать R в фоновом режиме).
Создайте новый R-скрипт через меню File. В открывшемся окне мы будем писать свои простые команды и планировать эксперименты с последующим их анализом.
Я хочу обратить внимание на 2 вещи:
- во-первых, пользователи часто ошибаются, потому что команды в R чувствительны к регистру (например, команда
c(1, 2, 3, 4)создаст список с 4 записями, но если вы используете заглавнуюC(1, 2, 3, 4), то ничего не получится); - во-вторых, если вам понадобилась помощь, используйте команду справки
help().
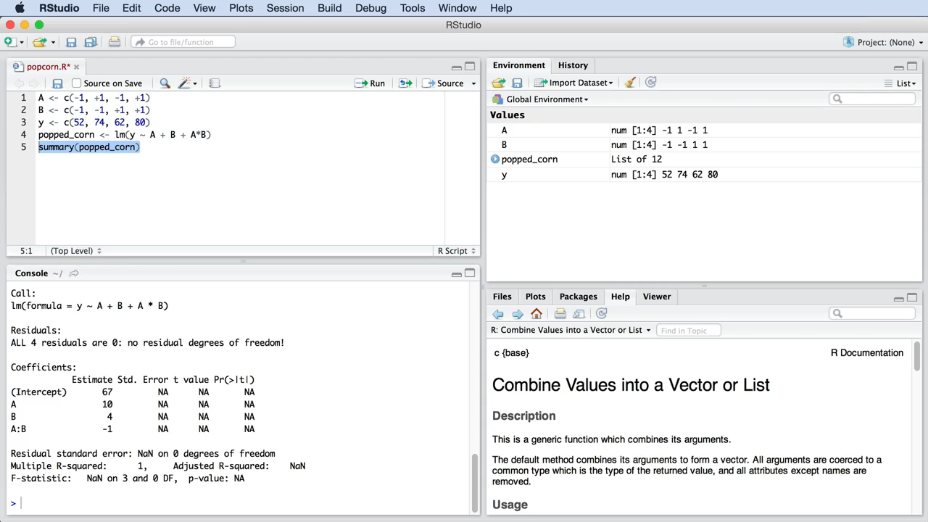
Пример, "попкорн-эксперимент" и рабочие области в RStudio показаны на рис. 7.
|
Рис. 7. "Попкорн-эксперимент" в RStudio. Изображены окна (слева на право и сверху в низ): написания скриптов, отображения переменных в памяти компьютера, консоль для вывода результата скрипта, окно справки по командам. |
В дальнейшем, вместо скриншотов, мы будем использовать просто код, который вы можете скопировать и выполнить у себя в RStudio:
A <- c(-1, +1, -1, +1)
B <- c(-1, -1, +1, +1)
y <- c(52, 74, 62, 80)
popped_corn <- lm(y ~ A + B + A*B)
popped_corn
Внимательные ученики могли обратить внимание, что запись эксперимента на картинке и в коде отличается и скоро мы узнаем почему.
Мы начнем с конца (своего рода обратная задача). Переменная popped_corn содержит в себе рассчитанные коэффициенты модели и просто выводит их в консоль (в этом и состоит смысл переменных, они являются ссылками на определенные значения или операции, которые мы присвоили им). Выше мы объявляем саму прогнозную модель под названием popped_corn. Если это ваше первое знакомство с R, вам может стать немного страшно - призываю быть мужественными и верь в свои силы!
Рассмотрим все по очереди. Начнем с обратной стрелки (<-). Это символы меньше (<) и тире (-), которые вместе похожи на стрелку. На языке R так выглядит операция присваивания (т.е. мы передаем переменной какое-либо значение и дальше можем просто писать переменную для использования этого значения). Другими словами, мы создаем переменную с именем popped_corn и присваиваем ей все, что находится справа от стрелки, в данном случае — линейную модель (точнее, результаты расчета линейной модели). lm справа от стрелки означает "линейная модель", указывая на то, что мы хотим получить линию методом наименьших квадратов. И наконец, символ в середине — тильду (~) — можно интерпретировать как "предсказывается ..." или "описывается ...".
Примечание. В R использование
<-и=практически эквивалентно, но я рекомендую использовать<-в качестве операции присвоения, чтобы избежать путаницы. Подробнее, можете почитать здесь.
Для запуска кода выделите все команды и нажмите Run или без выделения - кнопку Source (в модификации Source with Echo). Если мы не получили сообщение об ошибке в Console, то Вы увидите результат (тоже в консоли) и существующие переменные справа (Environment). Выходные данные этого небольшого кода показывают коэффициенты для построенной линейной модели.
Мы должны получить центральную точку (intercept) 67; основной эффект для А: 10 единиц; для B: 4 и эффект двухфакторного взаимодействия AB: -1. Обратите внимание, что эти числа точно соответствуют нашим расчетам вручную.
Вот и вся магия программирования. Это действительно самый быстрый и удобный способ получить модель с помощью компьютера.
Примечание. В формуле, описывающей линейную модель есть члены для A, для B и взаимодействия AB. Но, как вы могли заметить, в ней нет члена, отражающего центральную точку (константы). R создает его автоматически. Т.е. при вводе только трех параметров R покажет вам четыре.
На рис. 7 вы можете заметить команду summary(popped_corn), вместо простого вызова popped_corn. Эта команда позволяет получить расширенные данные по расчету параметров: погрешности определения коэффициентов, среднее квадратичное отклонение модели от экспериментов и т.д.. Более подробно с этими параметрами мы познакомимся во 2 и 3 частях нашего курса.
Примечание. В любой программе для расчетов вы должны получить точно такие же параметры для нашего эксперимента. Это хорошая проверка качества программного обеспечения и расчетов.
Задача. Попробуйте найти инструкцию в интернете как считать коэффициенты методом наименьших квадратов в MS Exel. В качестве примера используйте данные "попкорн-эксперимента".
Продолжим наше знакомство с R. Следующим примером будет расчет трехфакторного эксперимента по очистке воды.
Откройте RStudio и создайте новый файл для примера с очисткой сточных вод. Весьма логичным будет сразу задать нашу модель и затем объявить все необходимые переменные.
water <- lm(y ~ C + T + S + C*T + C*S + S*T + C*T*S)
Помните, что в примере с очисткой воды мы рассматривали три фактора: C (фактор "химиката"), T (фактор температуры) и S (фактор скорости перемешивания). Также у нас есть три двухфакторных взаимодействия (C*T, C*S и S*T) и одно трехфакторное взаимодействие (C*T*S). При этом у нас имеются результаты восьми экспериментов.
Примечание. При проведении эксперимента и анализе результатов следует помнить, что нам всегда потребуется провести как минимум столько же экспериментов, сколько неизвестных в нашей модели (сколько мы оцениваем параметров). Например, в "попкорн-эксперименте" было 4 параметра (2 единичных, 1 взаимодействие и один базовый) и 4 эксперимента. В примере с очисткой воды у нас есть 8 экспериментов, поэтому мы можем оценить 8 параметров (с учетом взаимодействия и базового значения).
Обратите внимание, что мы можем позволить R автоматически задать закодированные значения C, T и S, используя следующий код:
C <- T <- S <- c(-1, +1)
design <- expand.grid(C=C, T=T, S=S)
C <- design$C
T <- design$T
S <- design$S
water <- lm(y ~ C + T + S + C*T + C*S + S*T + C*T*S)
Первая строка задает три переменные сразу. Если мы проверим переменные, то увидим, что их значения -1 и +1. Далее, составим из них таблицу стандартного порядка для эксперимента, и извлечем столбцы значений C, T и S. Можете сравнить полученные значения с табл. 4 при ручном планировании эксперимента.
Теперь вы для каждого эксперимента можете пользоваться описанным подходом.
Последнее - нужно задать вектор результатов эксперимента (берем также из нашей таблицы 4):
C <- T <- S <- c(-1, +1)
design <- expand.grid(C=C, T=T, S=S)
C <- design$C
T <- design$T
S <- design$S
y <- c(5, 30, 6, 33, 4, 3, 5, 4)
water <- lm(y ~ C + T + S + C*T + C*S + S*T + C*T*S)
Запустите этот код, чтобы создать линейную модель. Для вывода рассчитанных коэффициентов в консоль используйте команду summary(water). Обратите внимание, что полученные значения параметров совпали с нашими расчетами вручную: 11.25, 6.25, 0.75 и т.д.
Примечание. Мы можем добавить небольшую хитрость, что бы задать нашу модель (это уменьшает возможность ошибки). Результаты модели будут аналогичны (прошу проверить).
# Используем упрощенную форму задания модели
water <- lm(y ~ C*T*S)
Примечание. При планировании каждого эксперимента всегда сами составляйте новый код и сохраняйте его. Так у вас останется некий "конспект" проделанной вами работы, и он будет особенно полезен, если вы будете использовать комментарии (строки, которые не воспринимаются программой как код, для R - начинаются с #). Это решит частую проблему потерю результатов и описания эксперимента. Например, вы провели работу, а через несколько месяцев вам нужно вернуться к ней и ответить на вопросы начальника или передать этот проект вашему коллеге. Если вы дадите им только файл Excel или набор документов, в которых нет пошагового описания, то будет очень сложно воспроизвести ваши действия и ход ваших мыслей. Я очень часто с этим сталкиваюсь в своей практике и призываю вас не повторять моих и чужих ошибок!
Написание хорошо закомментированного и последовательного кода создает хорошо прослеживаемую и воспроизводимую запись вашей работы. Это очень важный критерий для многих компаний и лабораторий (в некоторых даже существуют специальные требования к прослеживаемости результатов работы, например ISO 9001-2015).
Вот еще один фрагмент кода, который поможет нам в интерпретации результатов эксперимента. Он позволяет визуализировать влияние каждого из эффектов в полученной модели (чем больше абсолютное значение параметра перед кодированным фактором, тем больше его влияние).
# Оценка значимости факторов. Предварительно установите пакет "pid" Tools -> Install Packages -> pid
library(pid)
paretoPlot(water)
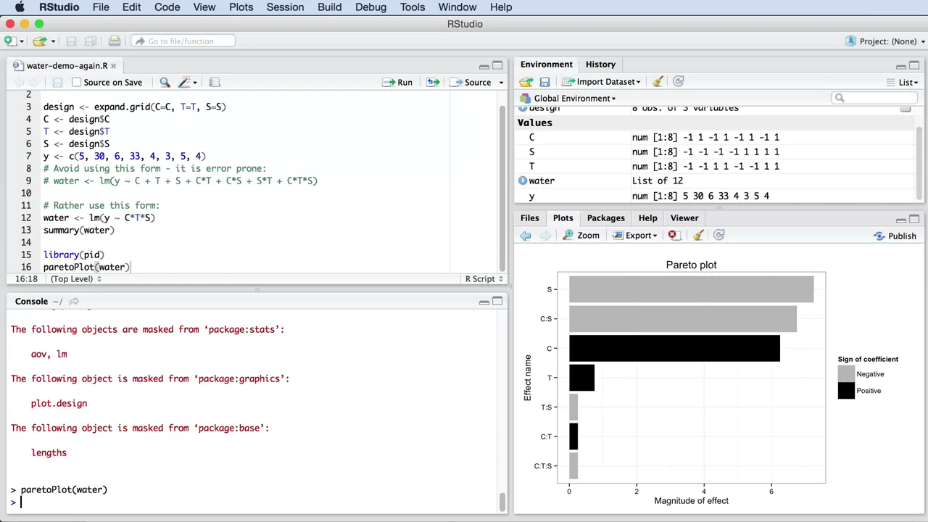
Результаты выполнения кода приведены на рис. 8.
|
Рис. 8. Пример сравнения факторов по диаграмме Парето (Pareto plot) в RStudio. |
Гистограмма показывает абсолютное значение каждого из параметров модели (это позволяет оценить масштаб влияния каждого из признаков). Знак коэффициента перед признаком тоже важен, он показывает направления влияния признака. Но для лучшего визуального сравнения правильнее использовать абсолютные значения (знак при этом выделен другим цветом). Такие диаграммы часто используются для определения неинтересных для нас переменных, которые потом можно удалить из модели. Гистограмма показывает параметры, отсортированные от наибольшего до наименьшего абсолютного значения. Это позволяет быстро находить наиболее важные факторы системы. Самые длинные полосы соответствуют факторам, наиболее значительно влияющим на результат.
Примечание. Часто важно использовать наглядное черно-белое сравнение, поскольку не все люди различают цвета. Кроме этого, иногда приходится печатать отчет на черно-белом принтере.
Проведем анализ построенной диаграммы. Сразу можно заметить, что взаимодействие \(C \times T \times S\) и взаимодействия \(C \times T\) и \(T \times S\) малы по сравнению с другими параметрами. Наиболее значимым является фактор S. Цвет полосы указывает на то, что S оказывает на результат отрицательное влияние. Как вы помните, наша цель заключалась в минимизации загрязнения, поэтому мы сразу понимаем, что увеличение S приведет к уменьшению загрязнения, что хорошо. Другим значимым фактором является эффект от химиката, C. Его влияние уже положительно, т.е. если мы выберем положительное кодированное значение этого категориального признака, то получим увеличение загрязнения.
Рассмотрим еще более сложный пример - четырехфакторный эксперимент с 2 измеряемыми параметрами. Это хорошая задачка из учебника Бокса, Хантера и Хантера. В этом эксперименте мы используем солнечные коллекторы и теплоаккумуляторы. Значения результата эксперимента получены из компьютерной симуляции и приведены на сайте.
Примечание. Небольшой совет, относящийся к симуляциям. Обычно проводить симуляцию очень просто и возникает искушение исследовать ее неэффективно. Часто можно встретить людей, которые просто играют с ПО, вводя разные значения, пока не получат нужный ответ. Но к симуляции следует относиться так же серьезно, как и к реальной модели. Всегда используйте систематический подход и проводите факторные эксперименты.
Примечание. Есть два ключевых преимущества использования компьютерных симуляций:
- быстрый результат при достаточной вычислительной мощности компьютера (или запуска в параллельном режиме);
- можно не рандомизировать порядок экспериментов. И причина этого довольно проста - как правило в симуляциях отсутствуют случайные и систематические ошибки, которые зависят от времени проведения эксперимента. Когда вы повторяете симуляцию при вводе одинаковых начальных значений вы получаете одинаковый ответ. Но будьте осторожны: некоторые компьютерные эксперименты при повторении не дают идентичные результаты и в любом случае - лучше всегда использовать случайный порядок. Затраты на это минимальны, но это защитит вас от ряда проблем.
Итак, вернемся к солнечному водонагревателю. Рассматриваем четыре фактора:
- A — количество солнечного света (инсоляция);
- B — емкость теплоаккумулятора (объем бака);
- C — расход воды через абсорбер;
- D — прерывистость солнечного света (облачность).
С точки зрения влияние данных факторов рассматриваются две переменные результата:
- \(y_1\) — эффективность сбора энергии;
- \(y_2\) — эффективность передачи энергии.
Вы можете сразу определить, сколько будет проведено тестов, если у каждого фактора есть два уровня: низкий и высокий, то \(2^4 = 16\).
Итак, было проведено 16 тестов, время составить код для расчета модели:
# Solar panel case study, from BHH2, p 230
# ----------------------------------------
A <- B <- C <- D <- c(-1, +1)
design <- expand.grid(A=A, B=B, C=C, D=D)
A <- design$A
B <- design$B
C <- design$C
D <- design$D
# y1 - collection efficiently
y1 <- c(43.5, 51.3, 35.0, 38.4, 44.9, 52.4, 39.7, 41.3, 41.3, 50.2, 37.5, 39.2, 43.0, 51.9, 39.9, 41.6)
# y2 - energy delivery efficiency
y2 <- c(82, 83.7, 61.7, 100, 82.1, 84.1, 67.7, 100, 82, 86.3, 66, 100, 82.2, 89.8, 68.6, 100)
model.y1 <- lm(y1 ~ A*B*C*D)
summary(model.y1)
paretoPlot(model.y1)
model.y2 <- lm(y2 ~ A*B*C*D)
summary(model.y2)
paretoPlot(model.y2)
Примечание. Причина, по которой запись \(A \times B \times C \times D\) работает, заключается в принципе иерархии модели для R. Давайте рассмотрим простой пример: если вы написали только \(A \times B\), то R автоматически включит в модель фактор A и фактор B. В конце концов, не может быть двухфакторного взаимодействия \(A \times B\), если нет факторов A и B.
После исполнения кода нужно изучить полученные результаты. Для этого построим две отдельные линейные модели и диаграммы Парето (рис. 9): для эффективности сбора энергии y1 и для эффективности передачи энергии y2.
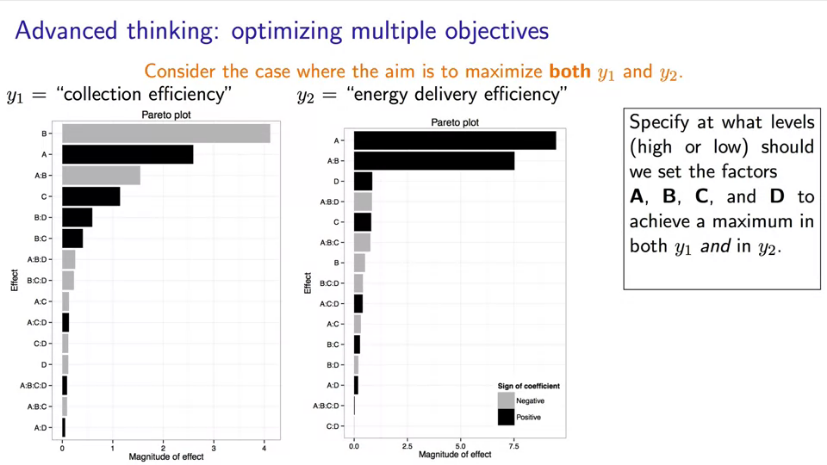
|
Рис. 9. Пример сравнения значимости факторов для рассчитанных моделей по диаграммам Парето. |
Как вы помните, серые полосы обозначают отрицательное влияние факторв на отклик, а черные полосы — положительное влияние. Согласно полученной модели для эффективности сбора энергии (\(y_1\)) наибольшее влияние у факторов B и A, взаимодействия \(A \times B\) и фактора C. Другие взаимодействия оказывают на результат более слабое влияние.
- Мы можем наблюдать уменьшение отклика при увеличении фактора B. То есть, когда объем бака увеличивается, эффективность сбора снижается. Это самая важная переменная в системе.
- Далее, фактор А (количество солнечного света), положительно влияет на эффективность сбора.
- Как вы думаете, какого рода будет эффективное взаимодействие \(A \times B\)? Правильный ответ — высокий уровень для фактора A и низкий — для фактора B. Мы видим это из уравнения и диаграммы Парето. В этом случае выбор низкого уровня фактора B повышает результат и одновременно заставляет двухфакторное взаимодействие работать в нашу пользу.
- фактор D слабо влияет на результат. Это полезный вывод, поскольку он показывает относительную нечувствительность к изменению облачности. Если бы в будущем нам предстояло провести дополнительные эксперименты, мы могли перестать учитывать фактор D. Аналогично, стремясь повысить эффективность сбора солнечной энергии y1, мы можем быть уверены, что облачность не будет играть значительную роль, по крайней мере, исходя из результатов анализа данной модели.
Таким образом, A, B и взаимодействие \(A \times B\) — три наиболее влиятельных параметре модели. Попробуйте объяснить влияние других факторов для этой модели самостоятельно.
Теперь посмотрим на вторую переменную результата — эффективность передачи энергии \(y_2\). Если изучить соответствующую диаграмму Парето, мы увидим следующее.
- Огромное влияние фактора A.
- Большое влияние двухфакторного взаимодействия \(A \times B\).
- Влияние факторов C и D не велико.
Объяснение - за вами.
Примечание. Вы могли заметить, что многие высокоуровневые взаимодействия (трех-, четырех- факторные и более) малы или равны нулю. Так бывает довольно часто и далее мы увидим как это можно использовать.
Примечание. На разобранном примере хотелось бы отметить важный момент. В случае модели \(y_2\) влияние фактора B мало и вы можете прийти к выводу, что фактор B не важен. Но это не совсем верно. Мы не можем исключить из модели этот фактор, потому что взаимодействие \(A \times B\) очень важно. Это означает, что влияние фактора A зависит от уровня фактора B и наоборот. Поэтому мы не можем игнорировать сам по себе мало значимый фактор B.
При рассмотрении подобного примера мы подходим к ключевому вопросу планирования экспериментов: можем ли мы одновременно оптимизировать оба результата \(y_1\) и \(y_2\)? Каково было бы лучшее сочетание уровней факторов, дающее этот максимум?
2.8 Сокращение затрат на эксперименты
Прежде чем ответить на вопрос об оптимизации модели, нужно понимать как оптимизировать фактор затрат на сами эксперименты.
Как можно заметить, в зависимости от количества факторов количество экспериментов (а значит время и стоимость) увеличиваются в степенной зависимости. Давайте попробуем избавиться от этого ограничения.
До сих пор мы рассматривали так называемые полнофакторноые эксперименты, когда для построения модели проводилось изучения влияния каждого фактора. Другими словами, мы исследовали каждое изменение каждого фактора. Но как можно сократить количество экспериментов?
Это возможно с использование кратного 2 сокращения числа экспериментов - например, использование half-factor (полуфакторного) эксперимента. Это подразумевает сокращение количество проводимых экспериментов вдвое!
Естественно, у всего есть цена, и подобные действия приведут к сокращению информации. Но для выбора этого пути есть 2 значимые причины:
- Стоимость каждого эксперимента может быть высока.
- Нет уверенности в результатах эксперимента, которые мы получим (какие факторы окажутся значимыми, будут ли полученные данные оптимальными и т.д.).
Согласно мнению известного ученого George Box для первых экспериментов и работ должно быть выделено около 25 % общего бюджета и не более. Остальное понадобиться нам в процессе последующего исследования. Таким образом необходимо понимать, что наши первоначальные предположения не абсолютны и вполне могут оказаться ошибочными. А значит нужна страховка и возможность дополнительного проведения новых экспериментов.
Давайте изучим, к чему приведет сокращение проводимых опытов вдвое (half-factor) и как это сделать.
Существует специальная схема выбора значимых опытов (тестов) из нашего идеального полнофакторного эксперимента: выбор по открытому или закрытому контуру. Рассмотрим знакомый нам пример по очистке воды с точки зрения выбора половины тестов (рис. 10).
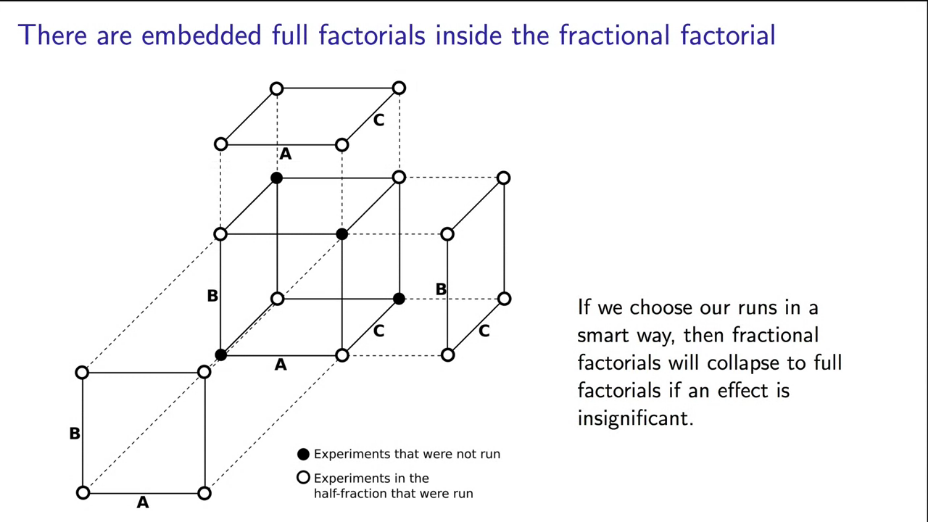
|
Рис. 10. Выбор значимых комбинаций для проведения half-factor эксперимента по одному из контуров (можно выбрать симметричный). |
Примечание. Значения признаков изменены на A, B, C для большего удобства.
Обратите внимание, что такой выбор экспериментов подразумевает полное изменение факторов А и В, а фактор С выбирается как результат перемножения первых кодированных факторов (с сохранением знака, как на рис. 10).
Такой подход к проведению эксперимента позволяет нам выиграть джекпот, если один из факторов окажется не важным для модели. Тогда одно из направлений куба исчезнет и мы вдвое сократим необходимое количество экспериментов, а с проведенными ранее у нас получиться полнофакторный эксперимент... Профит!
Но это только одна сторона медали. Давайте посмотрим, какая модель у нас получится, если мы проводим полуфакторный эксперимент:
# Half-factor experiment
# ----------------------------------------
# full-factors for A and B
A <- c(+1, -1, -1, +1)
B <- c(-1, +1, -1, +1)
# C = AB
C <- c(-1, -1, +1, +1)
# y - purify efficiently
y1 <- c(30, 6, 4, 4)
water <- lm(y1 ~ A*B*C)
summary(water)
При выполнении можно обратить внимание, что все взаимодействия признаков обозначены как NA (not applicable) - это предсказуемый результат. Модели не хватает данных. Но и нам не понадобятся данные факторы. Сравним полученное уравнение с исходным:
Обратите внимание, что 3 из 4 коэффициентов весьма близки по значению, хотя коэффициент В предсказан неверно и у нас нет информации по взаимодействиям факторов.
Разберем подробнее, что же происходит при half-factorial эксперименте.
Мы уже описали логику выбора необходимых сочетаний факторов. Однако обобщенное представление о выборе коэффициентов для проведения half-factor или еще более сокращенных экспериментов мы можем получить из специальной таблицы (trade-of-table, рис. 11).
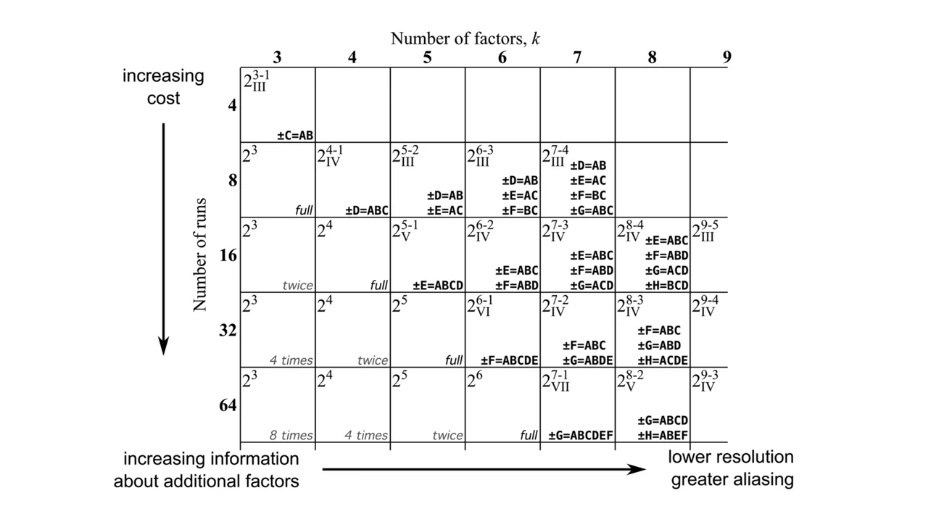
|
Рис. 11. Trade-of-table для выбора необходимых факторов при проведении half-factor эксперимента. |
Или используя следующий вызов в R:
library(pid)
help(tradeOffTable)
Далее мы еще вернемся к изучению этой таблицы, а пока будем подсматривать в нее, чтобы выбирать как кодировать наши факторы.
Следующий интересный вопрос - что же представляют собой новые коэффициенты и почему они отличаются от полнофакторного эксперимента? Это ключевой момент для понимания. На самом деле - коэффициенты в half-factor эксперимента являются комбинацией элементов из полнофакторного эксперимента! Рассмотрим это на примере очистки воды.
При полнофакторном эксперименте мы имеем следующую систему уравнений:
Теперь проведем математические рассуждения и оставим только выбранные эксперименты:
Еще раз повторю - это не строгое математическое доказательство, данные рассуждения нужны нам, чтобы показать логику.
Из последнего вектора с коэффициентами мы не можем убрать ни один, поскольку каждый из них соответствует изменению фактора, т.е. длине матрицы X, которая остается неизменной. Отмечу, что такая матричная запись умножения не имеет смысла (необходимо, чтобы размерность матрицы \(X\) соответствовала размерностям векторов \(y\) и \(b\)). Однако она поможет нам с логикой рассуждений, ведь для приведения к корректному виду матричного умножения (и самой системы линейных уравнений) необходимо сократить размерность матрицы \(Х\). Для этого обратим внимание, то столбцы этой матрицы на самом деле дублируются. Иными словами, части коэффициентов соответствует одинаковая кодировка оставшихся факторов. За этим скрывается одинаковое влияние исследуемых факторов, которое мы не сможем отличить друг от друга в нашем эксперименте (с математической точки зрения они будут идентичны).
Таким образом, если мы запишем реальную матричную систему для half-fraction эксперимента, то полученные коэффициенты на самом деле будут линейной комбинацией (aliasing, confounding) коэффициентов полнофакторного эксперимента:
Иными словами, в наших новых коэффициентах помимо влияния "чистых" факторов A, B, C содержится влияние взаимодействия этих факторов. Этим и объясняется то, что программа выводит нам только 4 коэффициента и они отличаются от исходных коэффициентов полнофакторного эксперимента.
Примечание. Вернитесь к сравнению уравнений полнофакторного эксперимента и half-factor эксперимента и убедитесь, что новые коэффициенты на самом деле линейные комбинации истинных.
Таким образом мы сократили количество факторов, исключив из рассмотрения взаимодействия, но учли его в наших новых коэффициентах!
После того, как мы познакомились с full-factor и half-factor экспериментами, можно предложить 2 возможные цели эксперимента (и пути его планирования):
- сканирование (screening) - когда мы допускаем сокращения информации о системе (например, не учитываем взаимодействия или получаем некоторые некорректные оценки параметров) и проводим сокращенные факторные эксперименты. Это делается с целью получения общих представлений о взаимодействиях в системе.
- оптимизация (optimization) - проводит поиск оптимального значения отклика. При такой схеме не допускаются сокращения экспериментов и требуется проведение полнофакторного эксперимента (обычно базируется на сканирующем эксперименте).
Учитывая вышесказанное, перед оптимизацией всегда нужно проводить планирование и оценивать эффект от каждого фактора и их взаимодействия (сканирующие эксперименты). Вот несколько полезных предварительных умозаключений на примере очистки воды (полнофакторный эксперимент потребует 16 повторений, каждое из которые весьма затратно по средствам, при этом исследуются 3 фактора: A - температура, B - скорость перемешивания и C - химикат).
- Важно правильно кодировать свои факторы при проведении half-factor эксперимента. Это позволит получать максимально приближенные к реальности коэффициенты. Например при приведенном кодировании можно сделать вывод, что \(\hat{b_C} = b_C + b_{AB} \approx b_C\) поскольку можно предположить отсутствие взаимодействия между перемешиванием и температурой воды. Таким образом мы получаем четкое представление о влиянии выбора химиката на очистку воды.
- Стоит использовать несколько кодировок и посмотреть на предполагаемые результаты half-factor экспериментов (выбрать наиболее интересные).
- Всегда стоит сначала проводить half-factor эксперименты, оценить результаты, и только потом "допровести" полнофакторный эксперимент (если все устроит и понадобится дополнительная информация).
2.9 Построение карты эксперимента
На данном этапе мы рассмотрели все основные подходы к планированию эксперимента и научились оптимизировать трудозатраты. Теперь можно приступить к достижению основной цели данного курса - научиться оптимизировать эксперимент и построить полную карту планирования эксперимента. Но для этого необходимо разобрать еще несколько понятий.
2.9.1 Мешающие факторы (disturbances)
Я думаю все мы подсознательно понимаем значения данного термина. До сих пор мы рассматривали идеализированное представление об эксперименте и предполагали, что на результат влияют только учтенные факторы или их взаимодействие. Однако помимо этого существуют различные мешающие факторы - некоторые погрешности.
Можно классифицировать мешающие переменные по нескольким критериям:
- известные или неизвестные нам;
- которые мы можем контролировать и не можем контролировать;
- которые мы можем измерить или не можем измерить.
Задача. Придумайте примеры для каждого из перечисленных случаев.
Во многих случаях мы не можем контролировать или измерить мешающее влияние. В таком случае нужно использовать методы статистической обработки данных (о них мы подробно поговорим в 3 главе). На данном этапе важно понимать, что для минимизации влияния мешающих факторов необходимо следовать 2 правилам.
- Всегда проводите свои эксперименты в случайном порядке (обратите внимание, как мы составляем таблицы экспериментов). Это позволить обеспечить случайное влияние неучтенных факторов, а значит с ними можно будет работать как со случайными величинами и они не сместят наши измерения (хотя и добавят им разброса или другими словами - дисперсии).
- Всегда записывайте дополнительные факторы, которые можете измерить.
Важным понятием является мешающее влияние, которое можно измерить, но нельзя контролировать - ковариации (covariates). Эти ковариации вполне могут влиять либо на измеряемый параметр, либо на один из учитываемых факторов. С такими мешающими факторами можно работать 2 путями:
- Провести визуальный анализ влияния ковариаций на потенциальные выбросы в измеряемых величинах.
- Добавить ковариации в модель в качестве фактора.
Другим типом мешающих факторов являются помехи (noise) - не измеримые и не контролируемые, но вносящие вклад в измерения.
О том, как обрабатывать помехи и случайные погрешности мы поговорим в главе № 3 (основы статистики). На данном этапе мы рассмотрим только ковариации и общие пути учета возможных погрешностей в экспериментах.
2.9.2 Блокировка мешающего фактора при расчете модели
В предыдущем разделе мы разобрали основные мешающие факторы и описали их поведение. Теперь нужно разобраться как работать с мешающими факторами при построении модели.
В качестве примера рассмотрим разработку мобильного приложения. У нас есть приложение, которое нужно разместить на рынке. Для этого, нужно провести эксперимент и понять, в каком случае оно будет иметь наибольший спрос. Руководством выделены следующие ресурсы:
- тестовые группы из 2000 человек;
- процент использующих приложение после 60 дней (наша измеряемая переменная \(y\)).
Факторы, которые мы планируем исследовать, приведены в табл. 5.
Таблица 5. Исследуемые факторы при выводе приложения на рынок.
| Low level (-) |
Hight level (+) |
|
|---|---|---|
| A "Promotion" | 1 free-in-app upgrade | 30 days trial of all features |
| B "Message" | "CallApp" has your schedule available at your fingertips, on any device | "CallApp" features are configurable; only pay for the features you want |
| C "Price" | in-app purchase price is 89 $ | in-app purchase price is 99 $ |
Но если провести мозговой штурм поставленной задачи, то можно выделить возможные мешающие факторы:
- E: возраст пользователя
- N: пол пользователя
- S: тип интернет соединения пользователя (мобильный или wifi)
- R: количество свободной оперативной памяти
- F: доставляется ли рекламные сообщения рекламной сетью G или H
- D: тип телефона (Android/Apple)
Как вы думаете, какие из приведенных факторов являются помехами (не измеримые и не контролируемые), какие ковариациями (измеримые, но не контролируемые), а какие - ни то ни другое?
При построении точно модели действует общее правило - фиксировать все, что возможно, и изменять только выбранные факторы. Но как тогда быть с факторами, которые мы можем контролировать, но у нас нет средств для проведения всех экспериментов или они кажутся нам не значимыми (nuisance factor)?
В случае случайных фактором (ковариаций или шума) мы должны использовать алгоритмы статистики (глава 3) и рандомизировать проведение эксперимента. Но если в нашей системе есть систематически мешающий фактор, который мы можем измерить и контролировать, то мы можем построить модель с минимальным влиянием данного фактора.
Например, в нашем случае одним из таких факторов предположительно является тип ОС - мы можем его измерить и контролировать. Здесь все зависит от того, имеет ли значение данный фактор для экспериментатора. Например, если мы хотим использовать приложение только на конкретной ОС - то фактор точно не имеет значения и стоит его просто зафиксировать. Но если мы хотим распространять приложение вне зависимости от ОС, то фиксировать данный фактор мы не можем - нужно обеспечить рандомизацию экспериментов и оценить влияние данного фактора на модель. Такая процедура называется "блокировкой" (blocking).
Примечание. Чтобы понять, нужно ли блокировать фактор, достаточно ответить себе на вопрос: "должна ли моя система или процесс успешно работать с разными значениями мешающего фактора в будущем"? Если да - нужно планировать эксперимент с блокировкой данного фактора. Ели нет - то у нас хорошая степень контроля над системой и мы можем избежать мешающей переменной.
Если необходимо изучить фактор и провести его блокировку, то основное правило для планирования эксперимента - рассматривать блокируемую переменную как дополнительный фактор. Допусти у нас имеется 3 фактора A, B, C и мы проводим полнофакторный эксперимент (8 экспериментов). Теперь добавим к нему мешающую переменную также с 2 возможными значениями (-1 и +1) - тогда мы получим half-factor эксперимент.
Вернемся к нашему примеру и проведем эксперимент по блокировки мешающей переменной - типом ОС. В результате мы получили, что Android пользователи дольше используют приложение, а Apple - меньше и наши результаты можно свести в табл. 6. Обратите внимание на выбор кодировки для блокируемой переменной.
Таблица 6. Блокировка мешающего фактора при выводе приложения на рынок.
| A "Promotion" | B "Message" | C "Price" | D = ABC "OS" | Outcome | |
|---|---|---|---|---|---|
| 1 | - | - | - | - (Android) | y_1* = y_1 + g |
| 2 | + | - | - | + (iOS) | y_2' = y_2 - h |
| 3 | - | + | - | + | y_3* = y_3 - h |
| 4 | + | + | - | - | y_4' = y_4 + g |
| 5 | - | - | + | + | y_5* = y_5 - h |
| 6 | + | - | + | - | y_6' = y_6 + g |
| 7 | - | + | + | - | y_7' = y_7 + g |
| 8 | + | + | + | + | y_8* = y_8 - h |
А теперь немного математической магии! Исследуем проведенный эксперимент и убедимся, что у нас получилось заблокировать мешающую переменную при проведении half-factor эксперимента. Рассчитаем эффект от фактора А как среднюю абсолютную разность:
Заметим, что если раскрыть скобки в числителе, то эффекты от мешающего фактора (ОС) сократятся - а значит, мы учли в модели "чистое" влияние фактора А.
Это же будет работать и для других параметров и их взаимных влияний за исключением совокупного влияния ABC:
Мы только что разобрали наилучшую стратегию действия при блокировке мешающей переменной. В данном случае - это лучший из вариантов. Часто трехфакторное взаимодействие выражено слабо и мы можем им пожертвовать, чтобы свести влияние мешающей переменной на систему к минимуму.
2.9.3 Разбор линейных комбинация признаков и планирование сканирующих экспериментов
Казалось бы блокирование - частный случай планирования эксперимента, который нужно просто запомнить. Но это не так. Мы уже сталкивались с изучением проведения half-factor экспериментов и линейной комбинацией признаков и я надеюсь теперь вы убедились, что это очень полезный навык при изучении системы! Он позволяет нам экономить время и ресурсы при исследованиях. Для такого планирования существует системный подход и сейчас мы постараемся разобрать его.
Для этого нужно понимать как работают линейные комбинации признаков (в иностранной литературе это явление называется "псевдонимы", aliasing). Лучше всего делать это на реальном примере.
Допустим, вы управляете автоклавом для выращивания бактерий. Такие системы часто используются для различных отраслей промышленности, в том числе и при создании современных минеральных удобрений с биологическим эффектом для почвы. Подобная система работает продолжительное время и дорога в обслуживании. Если вы обслуживаете данную систему, то для исследования 5 факторов может потребоваться до года (всего 32 эксперимента)! Допустим, наш бюджет может покрыть три месяца работы с установкой, а это 9 экспериментов. Для полнофакторного эксперимента это всего ли 3 фактора. Однако вовсе не обязательно сокращать количество факторов при таком количестве экспериментов. Мы можем провести исследование гораздо большего их количества (до 7)!
Это так называемое планирование сканирующего эксперимента (screening design). При этом мы не планируем построить точную модель или оптимизировать систему. Нам нужно лишь оценить значимость каждого из факторов для системы и понять как она работает. Какие факторы стоит исследовать для дальнейшей оптимизации.
Сократить количество экспериментов нам поможет стратегия частичного факторного эксперимента (part-factor experiment). В нашем случае для не более 9 экспериментов и 5 факторов - четвертичного факторного эксперимента (quarter-factor). Мы рассмотрим 5 факторов для 8 экспериментов (табл. 7).
Примечание. Если есть возможность, то можно провести 9 эксперимент для более точного анализа. Его рекомендуется проводить первым (своего рода базовая линия). Все численные факторы нужно принять в 0 положении (между -1 и +1), в случае категориальных - выбрать одно значение для всех (-1 или +1). Этот первый (пробный) эксперимент - отличный способ найти все подводные камни при проведении практической работы (ведь сложно сразу реализовать качественный эксперимент на практике). Если эксперимент будет неудачен - его можно выбросить, но если он получиться - он улучшит модель.
Таблица 7. Проведение quarter-factor эксперимента с дополнительным пробным экспериментом (9-ым).
| Experiments | A "temperatire" | B "dissolved oxigen" | C "substrate type" | D = AB "agitation rate" | E = AC "pH" |
|---|---|---|---|---|---|
| 1 | - | - | - | + | + |
| 2 | + | - | - | - | - |
| 3 | - | + | - | - | + |
| 4 | + | + | - | + | - |
| 5 | - | - | + | + | - |
| 6 | + | - | + | - | + |
| 7 | - | + | + | - | - |
| 8 | + | + | + | + | + |
| 9 | + | 0 | 0 | 0 | + |
После проведения практических работ и получения результатов, останется разобраться со значениями полученных коэффициентов: какие линейные комбинации реальных параметров полнофакторной модели в них зашифрованы (aliasing). Однако, если для half-fraction эксперимента данные коэффициенты можно было легко разобрать, то здесь понадобится определенный системный подход (чтобы понять, что же скрыто в коэффициентах).
Итак, исходя из trade-off-table (рис. 11), мы можем представить значения факторов D и E в соответствии со значениями других факторов для quarter-factor эксперимента (8 экспериментов для 5 признаков). Например для признака D:
Тогда мы можем работать с этим представлением как с матричной формой (перемножаются соответствующие вектора):
Умножим обе части уравнения на вектор D:
При этом
Тогда:
Аналогично мы можем получить формулу и для признака E: \(E = AC => I = ACE\).
На основании полученных результатов и формируется наш систематический подход для анализа линейных комбинаций.
- Прочитать генераторы для дополнительных факторов из таблицы: \(D = AB\), \(E = AC\).
- Преобразовать генераторы к вектору идентичного вида: \(I = ABD\) \(I = ACE\).
- Приравнять все полученные значения: \(I = \dots\) для всех генераторов. В нашем примере мы получим: \(I = ABD = ACE = (ABD)(ACE) = BCDE\).
- Убедиться, что в уравнении \(2^p\) сочетаний (где \(p\) - степень изменчивости признака). В нашем случае это \(2^2 = 4\) - верно (\(I\) тоже считается).
Докажем уравнение в п. 3: \(I = II = (ABD)(ACE) = AABCDE = (AA)BCDE = IBCDE = BCDE\)
Задание. Повторите описанный вывод и план эксперимента для 6 факторов и бюджете для 15-20 экспериментов.
Настало время рассмотреть, как данные вычисления помогут нам понять линейные комбинации и "псевдонимы" на практике.
Допустим, мы построили модель для quarter-factor эксперимента и хотим узнать, какие взаимодействия содержатся в коэффициенте перед фактором B в полученной модели. Для этого нужно провести ряд нехитрых вычислений:
- взять рассчитанное выражение для генераторов
- умножить каждую из частей равенства на фактор B
- упростить выражение, используя перестановки и правило идентичности (\(AA = I, BB=I, \dots\))
Проведем анализ полученного выражения. Согласно полученным данным, фактор B будет связан (confounded, aliasing) со взаимодействиями между 2, 3 и 4 соответствующими факторами. Однако, учитывая малый вклад взаимодействий 3 порядка и выше можно упростить систему до:
Задание. Рассчитайте самостоятельно с какими факторами будут связаны новые факторы C, D и А?
Проведя аналогичные расчеты для прочих факторов нашего эксперимента, можно получить следующую таблицу линейных комбинаций для нашего quarter-factorial эксперимента с 5 факторами:
Наиболее неявным будет результат для фактора А, поскольку он связан с 2 взаимодействиями сразу. Обычно за данный фактор принимают наименее важный параметр системы (от которого ожидают наименьшего влияния или который легко зафиксировать в будущем). Дополнительно, если фактор А оказывает слабое влияние на какой-либо из факторов, их взаимодействие будет мало и позволит нам явно оценивать какой-либо другой фактор.
Отсюда вытекает важное понятие - разрешение эксперимента (resolution of the design). Это наиболее точный уровень взаимосвязи факторов для данного плана эксперимента. В нашем случае разрешение равно 3 (т.е. признаки всегда связаны с двухфакторным взаимодействием).
Закономерный вопрос - можно ли получить лучшее разрешение для нашего эксперимента (т.е. получить линейную комбинацию не с двухфакторным взаимодействием, а с использованием взаимодействия в 3 и более факторов, чтобы можно было пренебречь данным влиянием)? И ответ - естественно! Но чтобы узнать сколько факторов и экспериментов должно быть в таких экспериментах, нужно воспользоваться римской цифрой в trade-of-table (рис. 11). Именно в данной таблице приведено обозначение разрешения и пути увеличения чувствительности эксперимента.
Для закрепления материала рассмотрим задачу по проведению эксперимента с 6 факторами в количестве от 15 до 20 экспериментов. Вот план действий:
- Взять из таблицы значение генераторов для факторов при k=6 и 16 экспериментах (quarter-factoial эксперимент).
- Преобразовать генераторы к виду \(I = ABCE\) и \(I = BCDF\).
- Выписать уравнение для идентичности, исходя из правила \(2^p = 2^2 = 4\) члена: \(I = ABCE = BCDF = A(BB)(CC)DEF = ADEF\)
- Рассчитать взаимосвязи для каждого фактора quarter-factoial эксперимента:
Обратите внимание, что для данного эксперимента наиболее точная линейная комбинация с 3ех факторным взаимодействием, и это отличный план эксперимента! Мы сможем получить точное определение влияния фактора A на систему.
Простой способ запомнить связь разрешения с факторным взаимодействием:
- Если у вас разрешение 3, то 1 фактор VS 2ух факторное взаимодействие.
- Если разрешение 4, то 1 фактор VS 3ех факторное взаимодействие и 2ух факторное VS 2ух факторное.
- Разрешение 5 - 1 фактор VS 4х факторное взаимодействие, 3ех факторное взаимодействие VS 2ух факторное взаимодействие, 2ух факторное VS 3ех факторное.
Примечание. Небольшие практические советы. Как вы могли заметить, разрешение будет связано с точность информации о влиянии факторов на систему.
- Разрешение 3: отлично подходит для проведения сканирования (screening). Например, при разработке нового продукта, выявления неполадок в процессе (при изменении цеха/производственной линии и т.п.).
- Разрешение 4: используется для изучения и понимания системы.
- Разрешение 5 и выше: используются для оптимизации процессов, изучения сложных эффектов, разработке высокоточных моделей. Весьма дороги!
Таким образом, при планировании начального эксперимента стоит придерживаться следующего алгоритма действия:
- Определить количество исследуемых факторов и количество экспериментов (исходя из бюджета).
- Взять вид генераторов из таблицы.
- Выписать все уравнения для идентичности.
- Убедиться, что уравнение идентичности содержит \(2^p\) членов.
- Рассчитать вид линейных комбинаций (aliasing pattern).
- Являются ли выявленные взаимосвязи проблемой для системы?
- Если да: переназначить названия факторов или выбрать другую схему эксперимента (начать планирование заново).
- Если нет: можно начинать эксперимент.
Для начала исследования системы всегда используйте наибольшее число факторов при меньшем разрешении. Сканируйте систему и только потом отсеивайте факторы! Всегда используйте численное подтверждение незначимости фактора, а не просто догадки!
Пример. Рассмотрим сканирующий эксперимент для 7 факторов при 8 экспериментах (trade-of-table в помощь). Составим стандартную таблицу (табл. 8).
Таблица 8. Проведение сканирующего четверть-факторного эксперимента с дополнительным пробным экспериментом (9-ым).
| Experiments | A | B | C | D=AB | E=AC | F=BC | G=ABC | y |
|---|---|---|---|---|---|---|---|---|
| 1 | - | - | - | + | + | + | - | 320 |
| 2 | + | - | - | - | - | + | + | 276 |
| 3 | - | + | - | - | + | - | + | 306 |
| 4 | + | + | - | + | - | - | - | 290 |
| 5 | - | - | + | + | - | - | + | 272 |
| 6 | + | - | + | - | + | - | - | 274 |
| 7 | - | + | + | - | - | + | - | 290 |
| 8 | + | + | + | + | + | + | + | 255 |
Пройдем наш алгоритм:
- Определить количество исследуемых факторов и количество экспериментов (исходя из бюджета) - сделано.
- Взять вид генераторов из таблицы - сделано.
- Выписать все уравнения для идентичности:
- Убедиться, что уравнение идентичности содержит \(2^p = 2^4 = 16\) членов - сделано.
- Рассчитать вид взаимосвязей (aliasing pattern). Разрешение нашего эксперимента = 3.
- Является ли взаимосвязь приемлемой?
Для этого используем код RStudio:
A <- B <- C <- c(-1, +1)
design <- expand.grid(A=A, B=B, C=C)
# The 3 factors that form the base of our design
A <- design$A
B <- design$B
C <- design$C
# These 4 factors are generated, using the trade-off table relationships
D <- A*B
E <- A*C
F <- B*C
G <- A*B*C
# These are the 8 experimental outcomes, corresponding to the 8 entries
# in each of the vectors above
y <- c(320, 276, 306, 290, 272, 274, 290, 255)
# And finally, the linear model
mod_ff <- lm(y ~ A*B*C*D*E*F*G)
# It is better to uncomment and use this line instead:
# library(pid) <-- best to use this!
# But this embedded R script does not have the "pid" library.
# So we will load the required function from an external server instead:
source('https://yint.org/paretoPlot.R')
paretoPlot(mod_ff)
# Now rebuild the linear model with only the 4 important terms
mod_res4 <- lm(y ~ A*C*E*G)
paretoPlot(mod_res4)
Результат построения модели приведен на рис. 12.
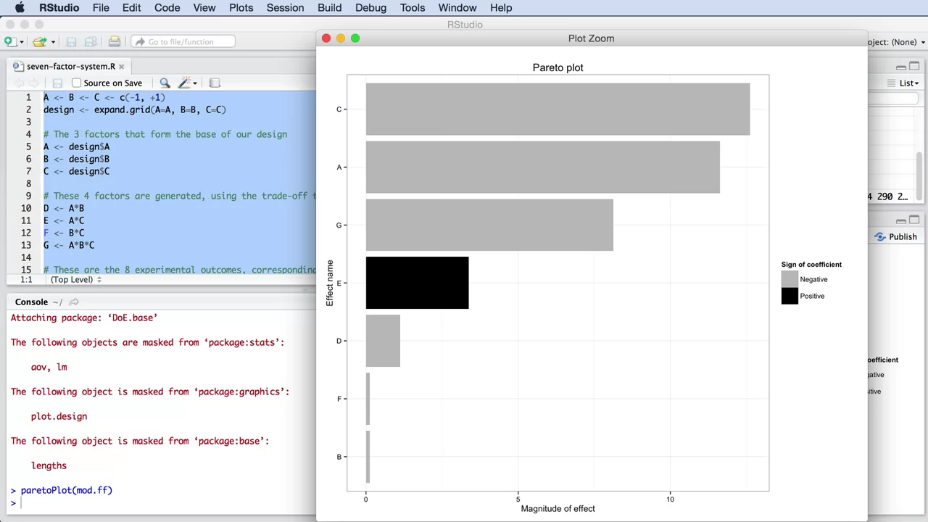
|
Рис. 12. Результат проведенного эксперимента. |
Как можно заметить, факторы C, A, G - значимы (отрицательный знак), чуть менее значим фактор E (положительный знак). Факторы D, F, B - незначимы и их можно удалить (при условии, что вы достаточно сильно варьировали их, чтобы оказать влияние на результат). При этом, мы понимаем, что каждый фактор на самом деле дополнительно включает в себя линейные комбинации.
Таким образом мы можем удалить из рассмотрения 3 фактора B, D, F, поскольку их влияние весьма мало (даже с учетом дополнительных взаимодействий). Мы можем перестроить модель без учета этих факторов и не проводя дополнительных экспериментов (рис. 13).
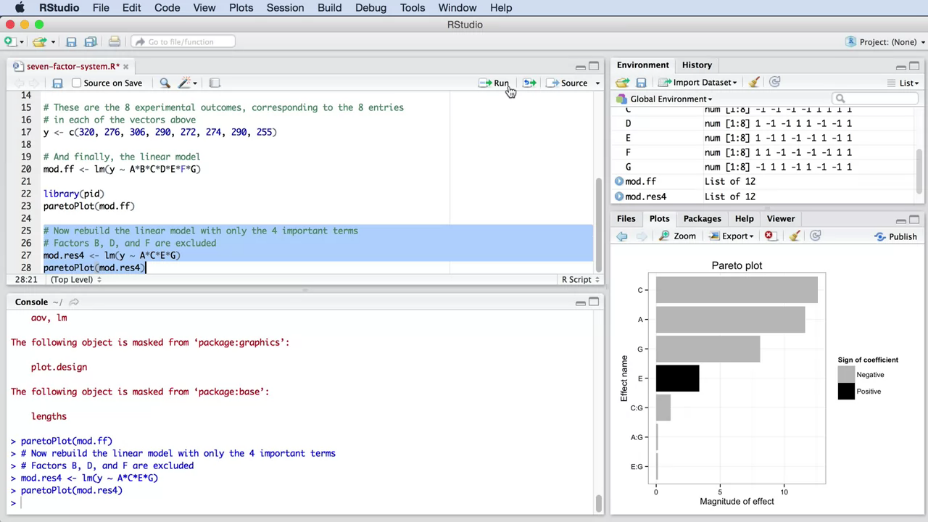
|
Рис. 13. Результат проведенного эксперимента после удаления незначимых факторов. |
Как мы можем убедиться, мы получили те же коэффициенты, что и до этого (из-за независимости столбцов матрицы факторов). Таким образом, мы можем удалить эти 3 фактора из рассмотрения. При этом мы сохранили 4 важных фактора которые предположительно влияют на модель и оценили двухфакторные взаимодействия, которые тоже оказывают влияние.
Примечание. Для тех, кто заинтересовался подобным планированием могу порекомендовать ознакомиться с дополнительными способами оптимизации экспериментов:
- Plackett-Burman design (для проведения экспериментов, количество которых кратно 4).
- "Definitive Screening Design" (тип оптимизационных критериев, например D-optimal designs). Могут быть очень гибкими.
2.9.4 Метод оптимизации поверхности отклика (response surface methods, RSM)
Мы достаточно подробно рассмотрели как можно блокировать мешающие и отсеивать не значимые признаки через правильное планирование и проведение сканирующих экспериментов. Время заглянуть за горизонт и понять, куда нужно двигаться после планирования и проведения факторного эксперимента. Именно за это отвечает метод поверхности отклика.
Но для начало нужно четко представлять зачем мы проводим свой эксперимент. В общем случае на это есть 5 причин:
- Получение дополнительной информации и изучение системы - разобрали.
- Выявления проблем - разобрали.
- Построение предсказания (модели) - разобрали.
- Оптимизация процесса - ?.
- Наблюдение за системой чтобы убедиться, что сохраняется прирост производительности - догадались.
До этого, мы рассматривали первые 3 пункта и немного затронули 4-ый (как вы думаете, когда?). Для этого мы исследовали систему, чтобы выявить значимые факторы и исключить не значимые (проводили скрининг). Это способствовало лучшему пониманию системы. Цитируя George Box:
"Discovering the unexpected is more important than confirming the unknown" (обнаружить неожиданное важнее, чем подтвердить неизвестное).
Можно сказать, что мы сможем решить примерно следующую задачу босса: "как работает данная система"? Вы устраиваете мозговой штурм и определяете 5-6 факторов, которые связаны с данной задачей (проблемой). Используя факторное планирование эксперимента вы можете быстро определить значимые и не значимые факторы и в принципе построить модель, которая предсказывает результат.
И в настоящей главе мы пойдем дальше и научимся решать следующую задачу босса: "теперь понято, как работает система, а как мы можем ее оптимизировать"? Для этого, после изучения системы нам понадобится расширить диапазон изменения факторов.
Для простоты рассмотрим немного измененный и ставший классическим эксперимент с попкорном. Рассмотрим 2 фактора: А - время готовки и В - тип масла. Откликом будет количество не сгоревших, но лопнувших зерен (далее вы увидите почему важно правильно выбирать отклик). Наша задача - максимизировать отклик. Результаты полнофакторного эксперимента приведены на рис. 14.
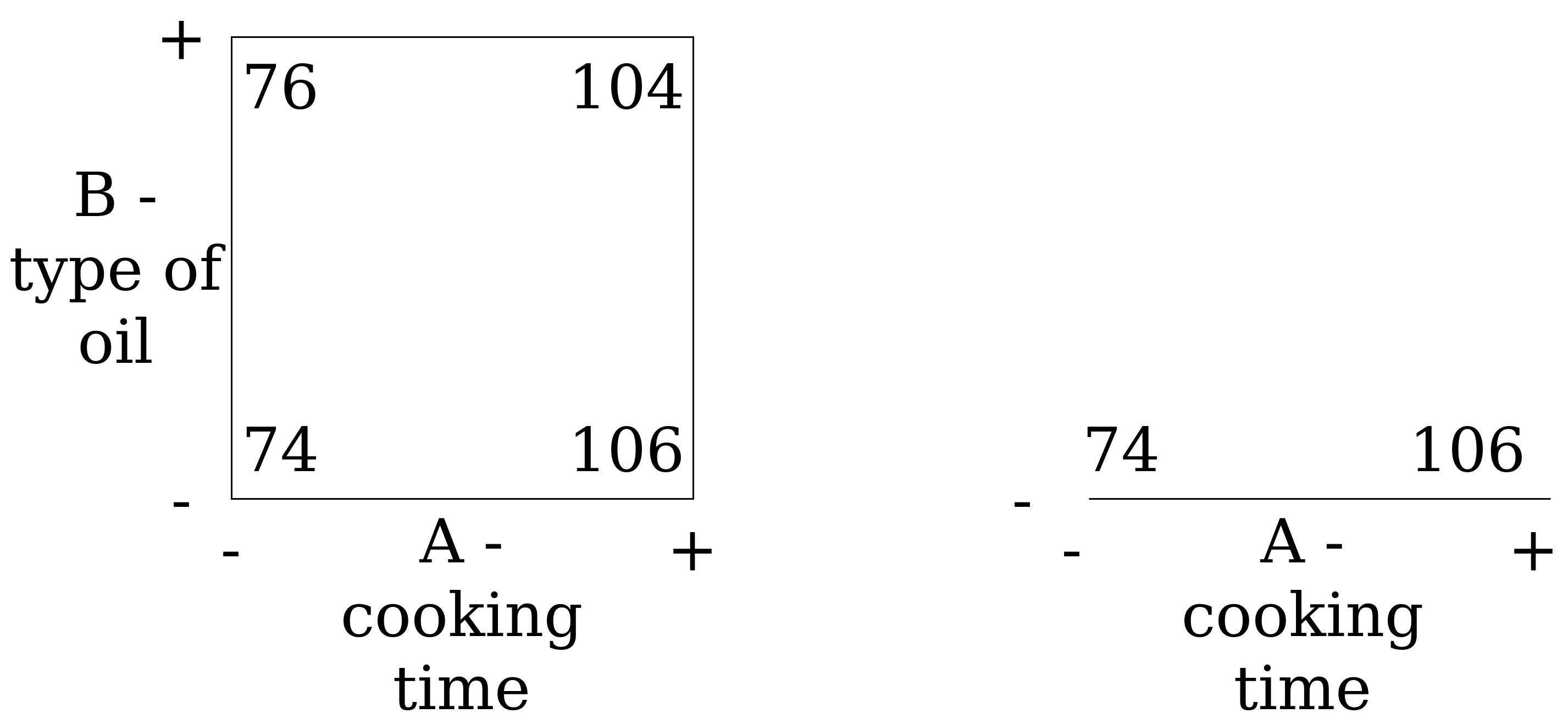
|
Рис. 14. Результат полнофакторного эксперимента. |
Как можно заметить, в нашем случае влияние масла практически не значимо по сравнению с влиянием времени. Таким образом мы можем свернуть наш квадрат до отрезка и модель будет чрезвычайно простой (фактор В и взаимодействие ВА приняты не значимыми):
Примечание. Отмечу, что все в мире относительно и масло конечно же влияет на наш отклик, но по сравнению со временем - влияет крайне не значимо.
Задача. Проведите данный расчет в RStudio самостоятельно с учетом обоих факторов и убедитесь в правильности предложенного упрощения.
Модель говорит нам, что при увеличении времени на 1 (т.е. от -1 до 0 и от 0 до +1, мы ведь кодируем время), количество не сожженных зерен увеличится на 15. И основная идея анонсированного метода оптимизационной поверхности как раз заключается в том, что эта модель говорит нам куда двигаться дальше. В нашем случае в сторону увеличения времени (рис. 15).
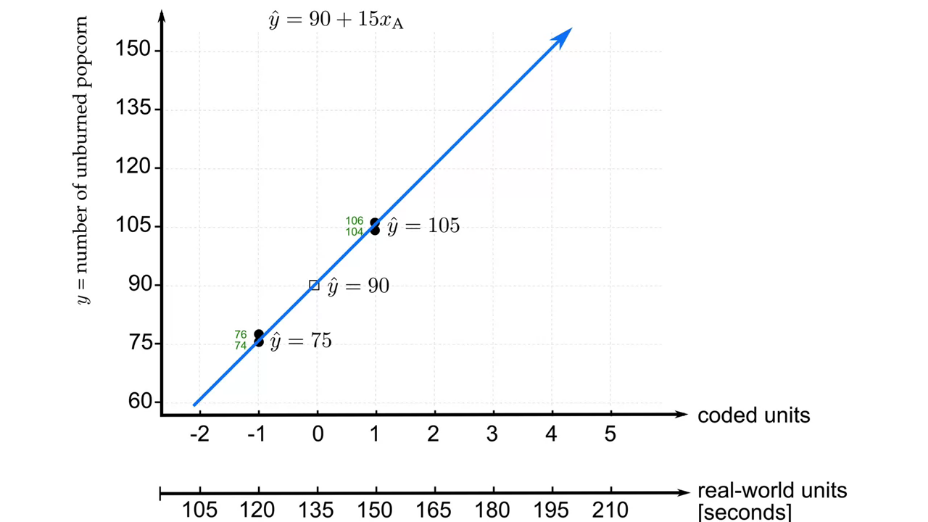
|
Рис. 15. Полученная модель для однофакторного "попкорн-эксперимента". |
Примечание. Данный метод оптимизации используется только после исключения всех незначимых факторов! Это важно. Никогда не включайте в оптимизацию незначимые факторы.
Примечание. Построенная модель (эмпирическая модель) никогда не скажет нам что произойдет за пределами граничных значений (за пределами рассматриваемого диапазона факторов)! Нет никаких математических и логических оснований для этого. Чтобы получить прогноз, нам нужно использовать метод оптимизационной поверхности и только после проведения сканирующего эксперимента.
Для проведения дальнейшего исследования нам понадобиться учесть следующие задачи:
- Разобраться как кодировать/декодировать физические единицы
- Определиться с линейными и нелинейными моделями
- Разобраться в степени доверия к моделями
- Ввести понятие шума и ошибки для эксперимента
- Понять как двигаться в сторону оптимума
- Обосновать выбор каждого дополнительного теста
Итак, мы часто говорили о кодировании и использовали кодовые значения переменных (-1, 0 и +1). Время ввести формальные формулы для расчета.
При кодировании:
При декодировании:
Примечание. Советую вывести данные формулы самим с использованием кубических диаграмм. Все довольно наглядно и один раз попробовав, всегда сможете вывести заново при необходимости.
Следующей задачей стоит разбор линейных и нелинейных моделей. Существует множество факторов выбора вида модели и критериев их выбора для каждого конкретного случая. Однако правило одно и оно было прекрасно сформулировано by George Box:
all models are wrong, but some are useful... the practical question is, how wrong do they have to be, before they are not useful? (перевод за вами)
Таким образом неважно, какую модель мы выбираем, важно - с каким диапазоном и с какими допущениями (ошибками) мы работаем. Любая гладкая функция может быть представлена в линейном виде в достаточно коротком диапазоне.
Но тут мы сталкиваемся с критерием оценки "полезности" модели - ошибкой (погрешностью). Причиной данного явления является шум (noise). Это те факторы, которые мы не контролируем и не можем измерить в данном конкретном случае. Простым подтверждением является проведение нескольких экспериментов при одинаковых условиях - мы получим разные значения отклика. Более подробно о погрешностях и методах их учета (статистике) мы поговорим в отдельной главе данного курса. А необходимый минимум мы уже рассмотрели ранее. Сейчас вернемся к основному вопросу: когда модель перестает быть нам полезной? Предлагаю ответ - когда она становиться не точной, другими словами когда ее предсказания начинают сильно отклоняться от эксперимента и это отклонение превышает допустимую погрешность.
На приведенном примере с попкорном, мы первоначально предположили линейную модель для кодированных значений -1 и +1 и определили направления оптимизации. Время провести следующий эксперимент. Двигаемся в сторону максимизации отклика и проведем новый эксперимент для закодированного значения фактора +2 (рис. 16).
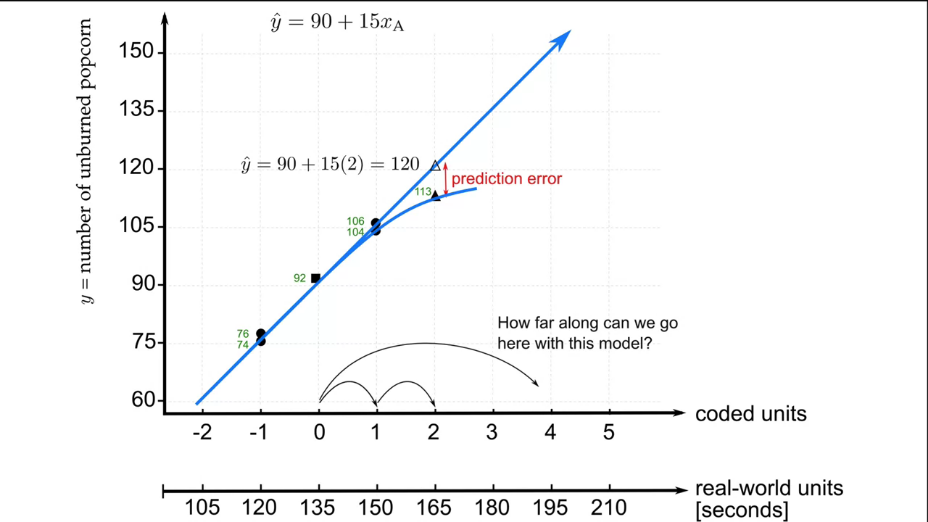
|
Рис. 16. Следующий эксперимент за пределами области определения модели. Оценка полезности. |
Предсказанное нашей моделью значение составит 120 зерен (предполагаемое значение), а в результате эксперимента мы получили 113 зерен... Полезна ли наша модель? Чтобы ответить на данный вопрос рассчитаем полученную погрешность:
Таким образом, если мы допускаем погрешность в 6.2 %, то полезна. Но это довольно большая погрешность, сравним ее с изначальной принятой нами погрешностью (когда исключили фактор масла):
Примечание. В первом случае мы рассчитали погрешность от экспериментального значения, поскольку считаем его более правильным. Во втором случае у нас нет наиболее верного значения, поэтому рассчитываем погрешность от среднего.
При сравнении с принятой погрешностью в 2.3 %, полученная погрешность в 6.2 % нас не устраивает. Время изменить модель.
Раз наша линейная модель перестала быть полезной - время разработать новую. Пойдем по одному из 2 возможных путей.
- Провести в точке расхождения новый полнофакторный эксперимент;
- Перейти к более сложной, нелинейной модели.
В нашем случае попробуем использовать более простой метод - модифицируем модель. Полный код с построением графиков приведен ниже
# Model for the popcorn system, ignoring factor B (oil type)
xA <- c(-1, -1, +1, +1)
y0 <- c(74, 76, 104, 106)
model.0 <- lm(y0 ~ xA)
summary(model.0)
# Plotting code: copy/paste and reuse this code as required
require("ggplot2")
raw_data <- data.frame(xA = xA, y = y0)
plot_data <- data.frame(xA = seq(-2, +5, 0.1))
plot_data$y <- predict(model.0, newdata=plot_data)
p <- ggplot(data=raw_data, aes(x=xA, y=y)) +
geom_point(size=10) +
xlab("Coded value for x_A") +
scale_x_continuous(breaks=seq(-2,5,1)) +
ylab("Outcome variable (number of unburned popcorn)") +
scale_y_continuous(breaks=seq(60,170,10)) +
theme_bw() +
theme(axis.text=element_text(size=26), legend.position = "none") +
theme(axis.title=element_text(face="bold", size=26))
p <- p + geom_line(data=plot_data, color="blue", size=1)
p
#ggsave("popcorn-linear-only.pdf", width=19.2, height=10.8, units="in")
# Now build the next model, model 1: y = 91.8 + 14.9 xA - 2xA^2
xA <- c(-1, -1, +1, +1, 0, +2)
y1 <- c(74, 76, 104, 106, 91, 113)
model.1 <- lm(y1 ~ xA + I(xA^2) )
summary(model.1)
predict(model.1, data.frame(xA=+1))
# Add these new model to the plot as a red line
plot_data <- data.frame(xA = seq(-1.5, +5, 0.1))
plot_data$y <- predict(model.1, newdata=plot_data)
p <- p + geom_point(aes(x=c(0), y=c(91)), shape=15, size=6)
p <- p + geom_point(aes(x=c(+2), y=c(113)), shape=17, size=6)
p <- p + geom_line(data=plot_data, color="red", size=1)
p
#ggsave("popcorn-linear-with-quadratic.pdf", units="in")
# Add the 7th and 8th point, and rebuild the model
xA <- c(-1, -1, +1, +1, 0, +2, +3.7, +5)
y2 <- c(74, 76, 104, 106, 91, 113, 116, 109)
model.2 <- lm(y2 ~ xA + I(xA^2))
summary(model.2)
plot_data <- data.frame(xA = seq(-1.5, +5, 0.1))
plot_data$y <- predict(model.2, newdata=plot_data)
p <- p + geom_point(aes(x=c(3.7), y=c(116)), shape=9, size=6)
p <- p + geom_point(aes(x=c(5.0), y=c(108)), shape=18, size=6)
p <- p + geom_line(data=plot_data, color="darkgreen", size=1)
p
Я специально привел довольно сложный код в котором рассмотрено несколько моделей и способ построения графика. Предлагаю Вам немножко потренироваться и разобраться что к чему (используйте RStudio или помощь в лекции №5В курса по планированию эксперимента).
В общем случае, при изменении модели на нелинейную мы добавили квадратичный член и получили новое представление общей модели (рис. 17).
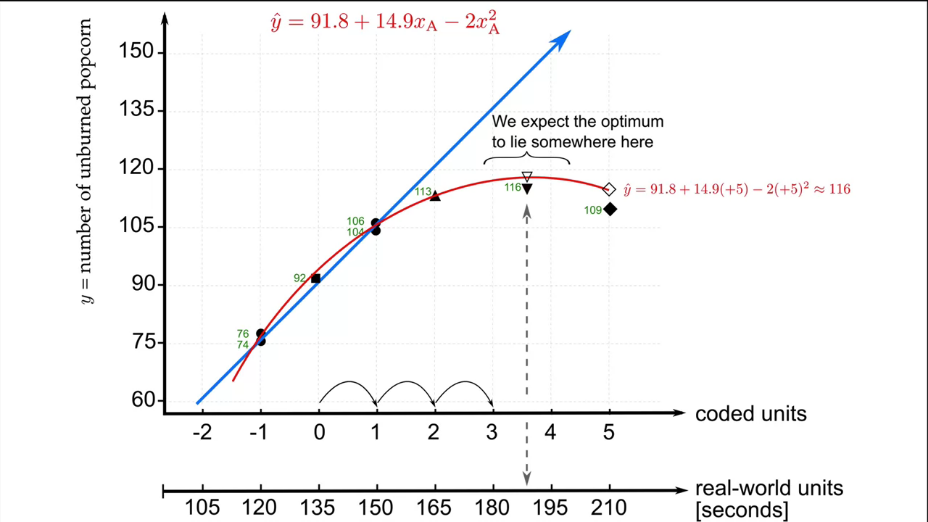
|
Рис. 17. Усложнение модели. |
Теперь погрешность нас устраивает и мы можем перейти к проведению следующего эксперимента. Для этого посчитаем, где должен находиться максимум (около 3.6 кодированных единиц, на реальные единица посчитайте сами).
При проведении нового эксперимента в предполагаемой точке максимума результат будет вполне удовлетворительный: 116 зерен против 118 по модели. Можно взять это значение за максимум.
Для подтверждения нашего предположения стоит провести дополнительный эксперимент около 5 кодированных единиц. При ожидаемом значении в 116, мы получили 109. Расхождение увеличилось, но тренд соответствует ожиданиям - максимум мы определили верно. Если хотите подстраховаться - можно перестроить модель по всем имеющимся данных (в коде это представлено) и посмотреть, как изменится положение максимума.
Таким образом мы рассмотрели простой пример оптимизации модели через последовательно проводимы эксперименты. Важно понимать, что перед проведением каждого последующего эксперимента мы должны понимать допустимую погрешность, выбрать шаг, рассчитать предполагаемое значение для выбранного шага и затем сравнить его с экспериментально полученным результатом. Затем - повторить цикл рассуждений.
2.9.5 Метод оптимизации поверхности отклика. Усложнение модели
Теперь, когда мы познакомились с основными понятиями и способами метода оптимизации поверхности отклика, можно двигаться в сторону усложнения и более реальных кейсов.
До сих пор, для метода оптимизационной поверхности мы использовали только один фактор. Такой подход называется COST (change one single thing) or OFAT (one factor at a time). Он прост, но абсолютно не дает представления о реальной картине.
- Он дает ложное представление об оптимуме, поскольку не учитывает другие факторы и их взаимодействия.
- Чем выше размерность эксперимента (количество факторов), тем больше шансов не приблизиться к реальному оптимуму.
Пример метода оптимизационной поверхности для случая с 2 факторами приведен на рис. 18.
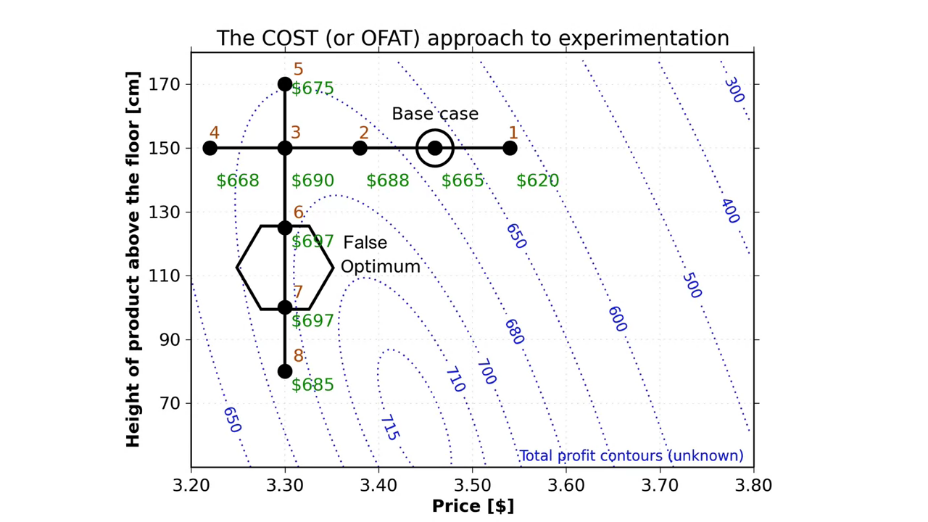
|
Рис. 18. Оптимизационная поверхность и контурные линии. |
В данном случае рассматривается прибыль в зависимости от цены на товар и высоты полки. Обратите внимание, что даже последовательное варьирование 2 факторов дало нам ложное представление об оптимуме для прибыли. Само же значение прибыли обозначено контурными линиями (линии при которые прибыль остается неизменной).
Проблема заключается в том, что установить контурную поверхность для отклика крайне затратно.
Для дальнейшего изучения мы будем использовать следующий случай. Нам нужно оптимизировать производство промышленной продукции. Наши факторы:
- количество продукции в час (T, throughput);
- цена единицы продукции (P, price).
Откликом будет прибыль (\(profit = \text{all income} - \text{all expenses}\)).
Допустим у нас есть некая точка отсчета (то, как работает цех сейчас) и мы проводим полнофакторный эксперимент вокруг нее (рис. 19).
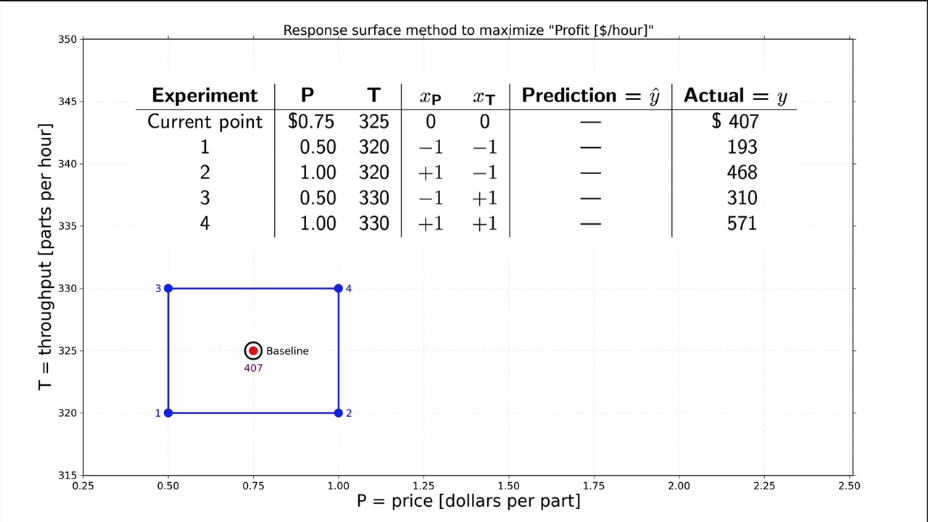
|
Рис. 19. Первоначальный полнофакторный эксперимент. |
Примечание. В рамках этой главы мы обсуждаем с вами множество параметров планирования эксперимента. Но довольно мало времени уделяем выбору диапазона для изменения фактора. Обычно эта задача является специфично для того или иного типа факторов. Но все же есть несколько общих рекомендаций для выбора диапазона изменений признаков.
- Вы должны иметь возможность экспериментально определять разницу между высоким и низким уровнем фактора:
- слишком узкий диапазон - вы будете измерять шум;
- слишком широкий - высока вероятность нелинейности.
- Не используйте значения близкие к экстремальным (исходное полотно на рис. 19, где цена ограничена здравым смыслом и рынком, а производительность - характеристиками системы).
- Если совсем нет идей - берите 25% от экстремального размаха (абсолютный максимум - абсолютный минимум фактора). В нашем случае - это 10 единиц продукта в час (если считать от 300 до 350).
После проведения факторного эксперимента нам понадобятся изолинии, которыми мы пользовались для кубических диаграмм (исходный код):
library(pid)
manufacture(P=1.05, T=325) # simulates a price of $1.05,
# and a throughput of 325 parts per hour
help(manufacture) # Gives you more details
rm(list = ls()) # clear the workspace of all prior variables
P <- c( 0, -1, +1, -1, +1)
T <- c( 0, -1, -1, +1, +1)
y <- c(407, 193, 468, 310, 571)
mod.base.1 <- lm(y ~ P*T)
summary(mod.base.1)
# You will need the PID package to run this code.
# Run the following command once, then you can comment this out again
install.packages("pid")
# Load the PID package in R.
library(pid)
contourPlot(mod.base.1, "P", "T")
# predict the points, using the model:
predict(mod.base.1, data.frame(P=P, T=T))
# Second factorial: points 4, 5, 6, 7 and 8 (baseline)
# ----------------
P <- c( 0, -1, +1, -1, +1)
T <- c( 0, -1, -1, +1, +1)
y <- c(657, 571, 669, 620, 710)
mod.base.2 <- lm(y ~ P*T)
summary(mod.base.2)
contourPlot(mod.base.2, "P", "T")
# Predict directly from least squares model, for experiment 9
predict(mod.base.2, data.frame(T=0.75, P=1.5))
# Step further, out to point number 10
P_coded = (1.63 - 1.18)/(0.5*0.36)
T_coded = (339 - 334)/(0.5*8)
predict(mod.base.2, data.frame(P=P_coded, T=T_coded))
# Third factorial: around baseline of point 10; cp(1.63, 339) and range(0.36, 6)
# Add runs 11, 12, 13, and 14 around the baseline [video 5F uses this code]
P <- c( 0, -1, +1, -1, +1)
T <- c( 0, -1, -1, +1, +1)
y <- c(732, 715, 713, 733, 725)
mod.base.3 <- lm(y ~ P*T)
summary(mod.base.3)
contourPlot(mod.base.3, "P", "T", main="Regular design")
# Use only point 9 (and not run point 11): points 9, 10, 12, 13, and 14
# This could also have been considered a "botched design".
P <- c( 0, -1, +1, -1, +1)
T <- c( 0, -2/3, -1, +1, +1)
y <- c(732, 717, 713, 733, 725)
mod.base.4 <- lm(y ~ P*T)
summary(mod.base.4)
contourPlot(mod.base.4, "P", "T",
main="Botched design (with run 9, instead of 11)")
# You may absolutely include point 9, into the rest of the factorial
# to gain an extra degree of freedom.
P <- c( 0, -1, +1, -1, +1, -1)
T <- c( 0, -1, -1, +1, +1,-2/3)
y <- c(732, 715, 713, 733, 725, 717)
mod.base.4.extra <- lm(y ~ P*T)
summary(mod.base.4.extra)
contourPlot(mod.base.4.extra, "P", "T",
main="With an extra degree of freedom")
# Back to model 3: points 10, 11, 12, 13, 14
P <- c( 0, -1, +1, -1, +1)
T <- c( 0, -1, -1, +1, +1)
y <- c(732, 715, 713, 733, 725)
model.3 <- lm(y ~ P*T)
contourPlot(model.3,"P", "T", main="Factorial 3: using points 10 to 14")
# Let's use model.3: y = 723.6 - 2.5 x_P + 7.5 x_T -1.5 x_T x_P
# and predict operation at point 15
predict(model.3, data.frame(P=-2/3, T=+2))
# Demonstrate curvature effects due to omitting the interaction term
P <- c( 0, -1, +1, -1, +1)
T <- c( 0, -1, -1, +1, +1)
y <- c(732, 715, 713, 733, 725)
model.5 <- lm(y ~ P + T) # notice the model is different, but the
# coefficients are the same.
contourPlot(model.3, "P", "T", main="Contour plot WITH interaction term")
contourPlot(model.5, "P", "T", main="Contour plot with NO interaction term")
# This fictitious data forms a saddle (saddles do occur in practice!)
# Which side do you climb up? Top left, or bottom right? [answer: both!]
P <- c( 0, -1, +1, -1, +1)
T <- c( 0, -1, -1, +1, +1)
y.fake <- c(722, 715, 725, 740, 721)
model.6 <- lm(y.fake ~ P*T)
contourPlot(model.6, "P", "T", main="System with much stronger interaction")
# Create the central composite design quadratic model
# Start with the factorial points: 11, 12, 13, 14
P <- c(-1, +1, -1, +1)
T <- c(-1, -1, +1, +1)
y <- c(715, 713, 733, 725)
# Now append the 4 center points: 10, 16, 17, 22
P <- c(P, 0, 0, 0, 0)
T <- c(T, 0, 0, 0, 0)
y <- c(y, 732, 733, 737, 735)
# Then add the star (axial) points: 18, 19, 20, 21
P.exact <- c(P, 0, -1.41, 0, +1.41)
T.exact <- c(T, +1.41, 0, -1.41, 0)
# Now, the true location of the axial points isn't quite at +/- 1.41
# Let's be a little more precise (using the idea of "botched designs")
P.star.low <- (1.38 - 1.63)/(0.5*0.36)
P.star.high <- (1.88 - 1.63)/(0.5*0.36)
T.star.low <- (335 - 339)/(0.5*6)
T.star.high <- (343 - 339)/(0.5*6)
P <- c(P, 0, P.star.low, 0, P.star.high)
T <- c(T, T.star.high, 0, T.star.low, 0)
y <- c(y, 738, 717, 721, 710)
# Go fit the model with quadratic terms
model.7 <- lm(y ~ P*T + I(P^2) + I(T^2))
summary(model.7)
contourPlot(model.7, "P", "T")
# Predict value of point 15 (actual value was $735)
predict(model.7, data.frame(P=-2/3, T=2))
# Predict the value of optimum
predict(model.7, data.frame(P=-0.22, T=+1.46))
Рекомендую разбить данный код на блоки и исполнить его (можете воспользоваться онлайн версией R).
Как уже говорилось, мы ввели дополнительную возможность - отрисовку контурных линий:
library(pid)
contourPlot(mod.base.1, "P", "T")
Полученные график с контурными линиями поможет нам выбрать направления для скорейшей оптимизации - перпендикулярно контурным линиям. Вот пример того, как выглядят реальные линии в нашем случае и построенные нами (рис. 20, редкий пример того, когда мы можем сравнить истинные и предполагаемые контурные линии - в реальной практике такого не встретишь).
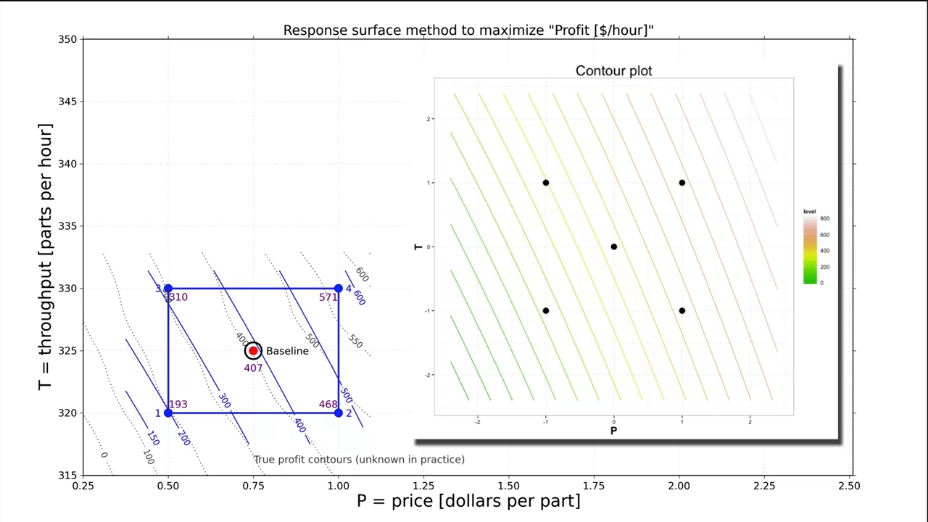
|
Рис. 20. Метод построения поверхности отклика для максимизации прибыли производства. Сравнение контурных линий. |
Итак, направление действительно выбрано верно. Всегда важно проверять экспериментальные значения на соответствие построенной модели. В крайнем случае, важно проверить хотя бы центральную точку. В идеале каждый из экспериментов следует повторить несколько раз, чтобы иметь представление об уровне шумов и повторяемости (но подробнее об этом в 3 главе).
Задание. Посчитайте относительные и абсолютные отклонения между построенной модели и экспериментальными данными.
После выбора направления нужно определиться с шагом для обоих факторов. Согласно нашей модели мы имеем уравнение:
Это значит, что при увеличении фактора P на 1 закодированную величину, профит увеличится на 134 единицы. В случае второго фактор - на 55 единиц. Тогда при одинаковом количестве шагов для факторов:
Таким образом в общем случае, для нахождения оптимума необходимо:
- Выбрать шаг для одного кодированного фактора (\(\Delta x_T = 1\)).
- Найти соответствующее изменение для другого фактора (\(\Delta x_P = \frac{b_P}{b_T} \cdot \Delta x_T = \frac{134}{55} \cdot 1 = 2.44\)).
- Преобразовать закодированные значения в реальные:
- Сделать шаги и установить место проведения следующего эксперимента:
- Посчитать предполагаемое значение согласно модели:
Однако при проведении эксперимента получилось значение в 669 долларов/час. Это сильное расхождение по обоим факторам (посчитайте, какое). Поэтому нужно спланировать новый факторный эксперимент в этой области, чтобы скорректировать направление. Есть несколько способов сделать это, основываясь на том где будет находиться полученная точка (эксперимент № 5).
Но наиболее экономичным является выбор, представленный на рис. 21.
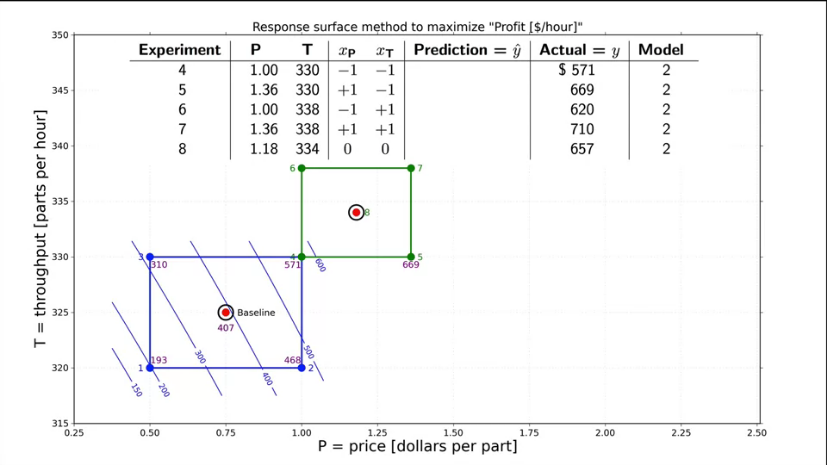
|
Рис. 21. Метод построения поверхности отклика для максимизации прибыли производства. Следующий факторный эксперимент |
Предлагаю вам самим подумать почему и продолжить логику рассуждения... Вы можете найти модель для данного эксперимента в интернете и реализовать любые свои задумки.
Итак, повторив рассуждения мы пришли к 9 эксперименту и выяснили, что расхождение с моделью составило: \(\Delta = 732 - 717 = 15\) \$ и это вполне приемлемый результат (строго говоря для этого нам нужно иметь представление о допустимой погрешности, но пока можем действовать интуитивно).
Таким образом, мы можем продолжить путь в выбранном направлении. Выберем шаг для 10 эксперимента, используя нашу последовательность действий.
- Выбрать шаг для одного кодированного фактора (\(\Delta x_P = 2.5\)).
- Найти соответствующее изменение для другого фактора (\(\Delta x_T = \frac{b_T}{b_P} \cdot \Delta x_P = \frac{22.5}{47} \cdot 2.5 = 1.2\)).
- Преобразовать закодированные значения в реальные:
- Сделать шаги и установить место проведения следующего эксперимента:
- Посчитать предполагаемое значение согласно модели:
Сравним с экспериментом (732). Это уже значимо, время перестроить модель.
Выберем 10 эксперимент в качестве новой базовой точки (0, 0). Диапазон для T возьмем немного меньше чем в предыдущем случае, поскольку:
- мы приближаемся к оптимуму и важно не перейти через него;
- предыдущие эксперименты говорят от уменьшении размаха, что также говорит о приближении к оптимуму.
Для фактора P оставим диапазон прежним, он не так велик, если сравнивать с общим размахом.
Отмечу, что выбор точного диапазона не так важен на практике, пока от позволяет приближаться к оптимуму. Это связано со статистической природой результатов эксперимента и тем, что в конце-концов, оптимум у нас один.
В результате новых экспериментов получим следующую картину (рис. 22).
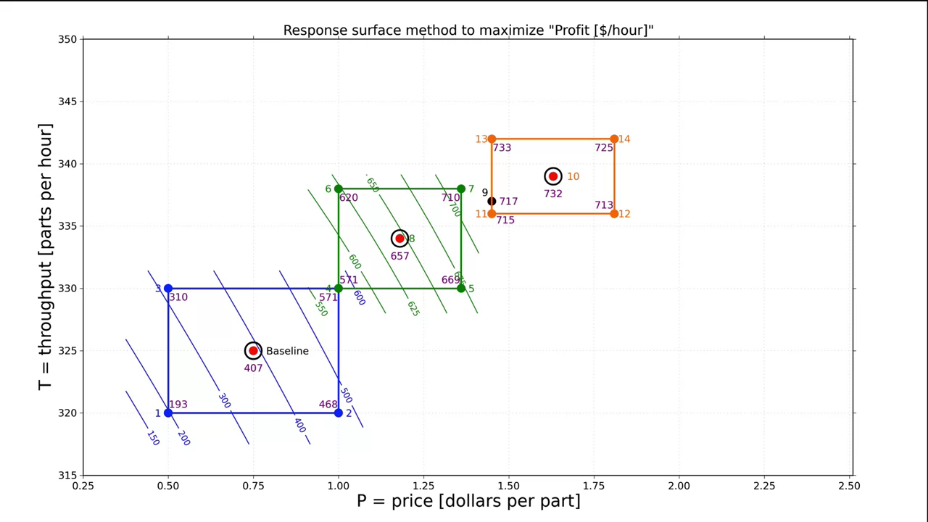
|
Рис. 22. Метод построения поверхности отклика для максимизации прибыли производства. Следующий факторный эксперимент. |
Не забывайте - все эксперименты в рамках факторного эксперимента проводятся в случайном порядке!
Если вы построите кубическую диаграмму с контурными линиями в RStudio, то заметите, что характер контурных линий изменился. Это явный признак изменения во влиянии признаков на отклик - сильно проявляется взаимодействие.
При этом вместо 11 эксперимента, мы могли бы использовать значение 9-ого, но с поправкой на кодировку (в данном случае не -1, а -2/3). Это называется планирование Боше (Botched design).
Задача. Используйте в коде расчет для полнофакторного эксперимента с 9 экспериментов вместо 11. Проверьте, получили ли вы ту же модель (не забудьте исправить значение кодировок)? Как Вы думаете, почему?
Кроме того, сама система координат часто имеет ограничения из-за которых приходится проводить несимметричные факторные эксперименты (поскольку оптимум часто находится на границе ограничений, рис. 23).
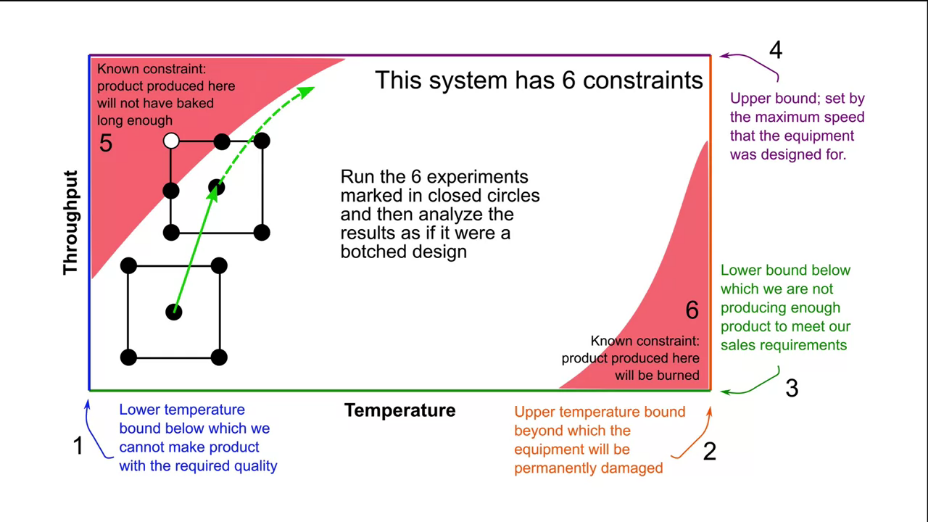
|
Рис. 23. Пример ограничений в системе, обеспечивающих ее несимметричность. |
Но вернемся к нашему эксперименту. Взаимодействие факторов меняет форму контурных линий, но направление нам известно. Давайте сделаем следующий шаг из предположения, что изолинии линейны (эксперимент № 15, рис. 24).
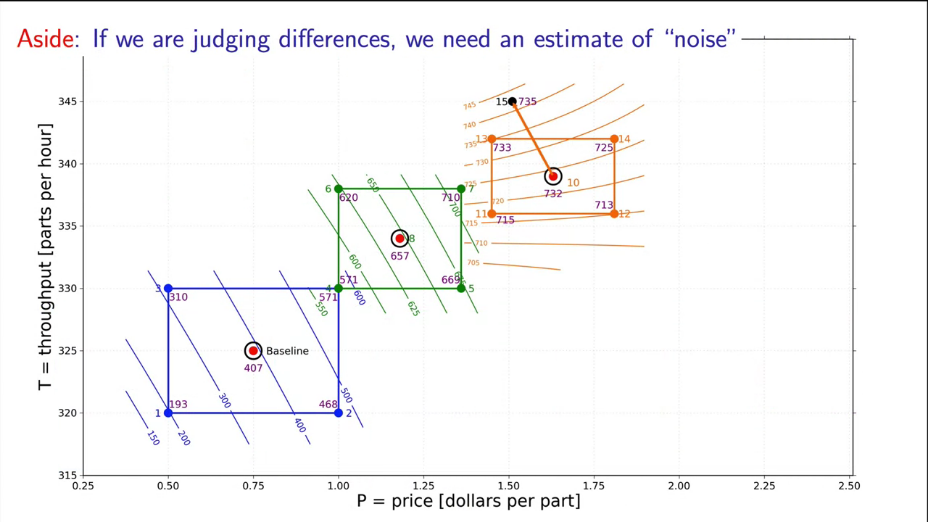
|
Рис. 24. Метод построения поверхности отклика для максимизации прибыли производства. Следующий факторный эксперимент в предположении, что контурные линии линейны. |
После проведения наших расчетов и получения экспериментальных данных разница составит: \(\Delta = 742 - 735\). Это больше нашего порога в 7 \$. Предположение игнорировать нелинейность контурных линий провалилось. Нам нужна другая стратегия.
Отметим, что приближаясь к оптимуму контурные линии вероятно будут изменяться и могут иметь разный вид в зависимости от силы взаимодействия (рис. 25).
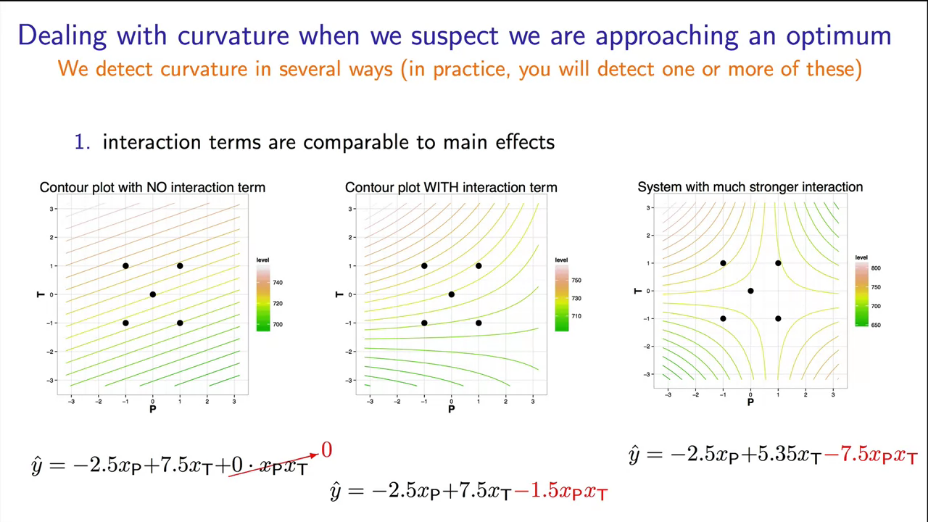
|
Рис. 25. Тип контурных линий в зависимости от взаимодействия факторов. |
Другим критерием приближения к оптимуму является уменьшение спреда отклика (\( \approx \text{размах}\)) между кодированными переменными в факторных экспериментах, даже если шаг выбирается адекватным (рис. 26).
|
Рис. 26. Зависимость спреда от приближения к оптимуму. |
Примечание. Строго говоря, в случае сперда важно понимание статистики и уровня шумов в нашей системе. Мы должны быть уверены, что разница в спреде обусловлена не шумом.
Для установления уровня шумов в системе необходимо несколько раз повторить один и тот же эксперимент. Допустим мы повторили 10 эксперимент 3 раза и получили значения в 732, 733, 737, что даст нам спред в 5 $. Что меньше, чем 20 $. Это говорит о том, что мы все еще видим сигнал, а не шум.
Третьим параметром приближения к оптимуму является величина расхождение модели с экспериментом. Если изменения значимы - мы все-еще можем улучшать модель и двигаться к оптимуму.
Четвертым фактором, указывающим на близость к оптимуму является проявление невозможности аппроксимации линейной моделью "lack of fit". Оптимум подразумевает точку перегиба.
Например, сравним различия для наших 3 факторных экспериментов.
- Модель: \(y = 390 + 134 x_P + 55 x_T - 3.5 x_P x_T\). Разница в базовой точке составила \(\Delta = 407 - 390 = 17\). В сравнении с коэффициентами модели довольно не много (что говорит о маленькой степени "lack of fit").
- Модель: \(y = 645 + 47 x_P + 22.5 x_T - 2.0 x_P x_T\). Разница в базовой точке составила \(\Delta = 657 - 645 = 12\). Меньше, но уже ближе к коэффициентам модели (что говорит об усилении "lack of fit").
- Модель: \(y = 724 - 2.5 x_P + 7.5 x_T - 1.5 x_P x_T\). Разница в базовой точке составила \(\Delta = 734 - 724 = 10\). Уже сравнимо с коэффициентами модели, при этом уровень шума в 5 \$ говорит о том, что это все еще сигнал, хоть и весьма зашумленный (сильный эффект "lack of fit").
|
Рис. 27. Демонстрация эффекта "lack of fit". На последнем полнофакторном эксперименте показаны 3 дополнительных эксперимента для определения уровня шумов. |
В случае нашего эксперимента все говорит о том, что пора сделать модель нелинейной (добавить квадратный член). Для этого есть 2 варианта:
- Добавить тест на стороне куба (face centered design, FCD) - применяется, когда мы не можем покинуть область куба.
- Добавить тест за рамками куб (the "original" central composite design, CCD) - предпочтительней со статистической точки зрения.
Мы же с вами ограничимся общими правилами:
- Провести последний полнофакторный эксперимент.
- Провести дополнительный тест на расстоянии \(\alpha = (2^k)^{0.25}\), где k - количество факторов.
- Провести несколько измерений базовой точки (максимально варьируя условия, включая время начала анализа).
С точки зрения 2 факторов в нашем случае получится 5 дополнительных экспериментов "вокруг" полнофакторного, что позволит нам построить точную нелинейную модель (рис. 28).
|
Рис. 28. Построение нелинейной модели. |
Теперь построим модель на основании полученных данных (время кода!) и рассчитаем отклонение. Предлагаю проделать это самостоятельно.
В результате 12 тестов: (4 факторных + 4 базовых точек + 4 дополнительных точек).
- Модель: \(y = 734.23 - 2.5 x_P + 6.97 x_T - 10.6 x_P^2 - 2.5 x_T^2 - 1.5 x_P x_T\)
- Мы получили хорошее предсказание в центре, которое говорит о малом эффекте "lack of fit": \(\Delta = 734.25 - 734 = 0.25\).
- Мы получили хорошие предсказания для прочих точек.
Теперь представим полученные результаты в виде контурных линий и убедимся, что мы действительно рядом с оптимумом.
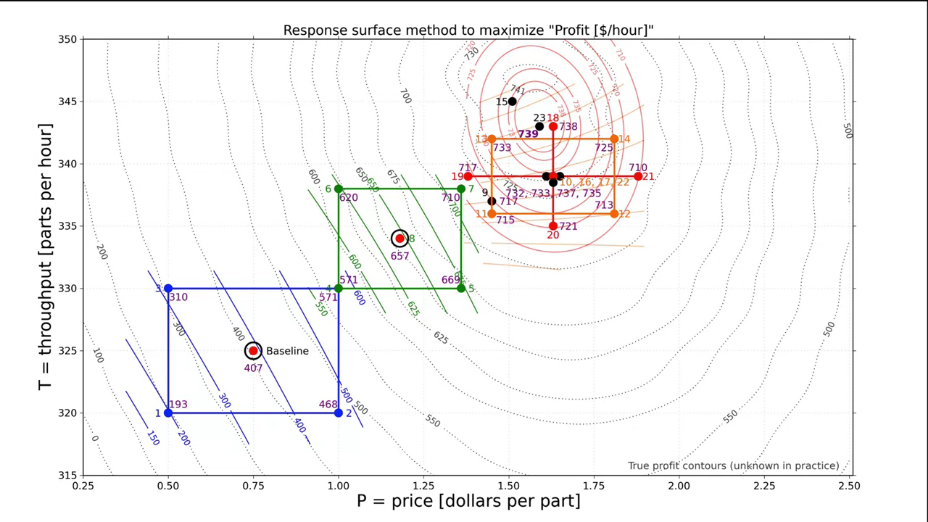
|
Рис. 29. Построение нелинейной модели. Контурные линии оптимума (рассчитанные и реальные). |
Эксперимент № 18 находится практически в оптимуме и на этом можно закончить оптимизацию. Но если бы мы не попали в оптимум - надо было провести дополнительные эксперименты по построению нелинейной модели в предполагаемом центре оптимума.
Примечание. Оптимум может меняться со временем (это зависит от исследуемой системы). Поэтому есть специальные системы, которые отслеживают такие передвижения. Если вам интересно - почитайте про "Evolutionary Operation (EVOP)".
Мы подошли к концу основной части данной статьи. Надеюсь мы узнали как планировать и проводить эксперименты с целью изучения и оптимизации системы. В следующих частях нас ждет более детальное знакомство со статистикой и линейной регрессией - основными инструментами анализа данных и построения моделей.
2.10 Заключение
В рамках настоящей главы мы познакомились с экспериментами, способами их планирования, проведения, построения моделей, анализа результатов и проведения оптимизации.
Подведем небольшое формальное заключение пройденного материала.
Существуют следующие задачи эксперимента:
-
Сканирование и изучение системы (измерительный процесс). Оценка значимых факторов изучаемого объекта, а также проверка некоторых гипотез, касающихся этих характеристик (например, влияет ли добавка некоторого компонента на прочность бетона и т.п.).
-
Задача регрессионного анализа. Установление функции отклика, т.е. статистически достоверной зависимости, связывающей отклик с факторами (построение математической модели изучаемого объекта). Это процесс разработки методики для анализа.
-
Корреляционный анализ. Определение степени взаимной статистической связи двух величин. Например, это оценка линейности градуировочного графика и т.д..
-
Экстремальный (оптимизационный) эксперимент. Нахождение оптимальных условий протекания процесса, т.е. определение значений факторов, при которых отклик является максимальным (или минимальным).
Основные стадии эксперимента на примере оптимизации системы (включает в себя большее количество стадий).
- Постановка задачи (определение цели и задач эксперимента, оценка допустимых затрат времени и средств, установление типа задачи).
-
Мозговой штурм задачи: оценка измеряемых и мешающих факторов, выбор переменной отклика системы (изучение литературы, опрос специалистов и т.п.).
-
Выбор способа решения и стратегии его реализации (типа факторного эксперимента). Корректирование сроков и бюджета.
-
Проведение сканирующего эксперимента при стандартных условиях эксплуатации системы. Обеспечение блокировки мешающих факторов. Оценка значимых и не значимых для модели факторов. Критическая оценка методики проведения экспериментов и полученной модели.
-
Реализация выбранного способа решения задачи (факторы, граничные условия, отклик и тип оптимизации, объем выборки, кратности повторения опытов и т. д.).
-
Проведение оптимизации методом оптимизационной поверхности. Анализ и интерпретация результатов, их представление для менеджеров и руководства (получение оценок интересующих экспериментатора величин и определение степени достоверности этих оценок, выражение результатов в конкретных и необходимых терминах).
Требования к фактору.
-
Управляемость - возможность придавать фактору любой уровень в области его определения и поддерживать этот уровень постоянным в течение всего эксперимента.
-
Однозначность - фактор не должен быть функцией других факторов (т.е. должен быть линейно независим).
-
Должен быть закодирован для правильной интерпретации полученной линейной модели. Выбранные для эксперимента количественные или качественные состояния фактора называются уровнями фактора (-1 и +1 в наших случаях). От числа уровней зависят объем эксперимента и эффективность оптимизации.
Зависимость числа экспериментов от числа факторов и количества их уровней имеет вид \(N = p^k\), где \(N\) – число опытов; \(p\) – число уровней факторов; \(k\) – число факторов.
Пространство, в котором строится поверхность отклика, называется факторным пространством. Оно задается координатными осями, по которым откладываются значения факторов и параметров оптимизации.
Истинным значением физической величины называется значение, которое идеальным образом отражало бы свойство объекта. Определить экспериментально его невозможно вследствие неизбежных погрешностей измерения.
Действительным значением физической величины называется значение, найденное экспериментальным путем и максимально близкое к истинному значению.
Измерением называется процесс нахождения значения физической величины опытным путем с помощью специальных технических средств.
Принцип измерений – совокупность физических явлений, на которых основано конкретное измерение.
Средство измерений – это техническое средство, предназначенное для измерений. Как правило с утвержденными метрологическими характеристиками (т.е. с данными, позволяющими оценить погрешность измерения).
Метод измерений – совокупность принципов использования определенного средства измерения.
Методика - конкретная последовательность действий (совокупность приемов) для измерения с использованием конкретного метода.
Погрешностью называется отклонение результата от истинного значения измеряемой величины. Т.к. истинное значение измеряемой величины неизвестно, то опираются на статистику. (при количественной оценке погрешности пользуются действительным значением физической величины).
2.11 Вопросы по разделу
- Ваша компания изучает влияние рекламны сообщений для своего мобильного приложения (например, рассылка SMS, отображение рекламных сообщений в приложении). Вы должны возглавить это исследование. Выберите все категориальные переменные.
- Использование 120 или 140 знаков в сообщении.
- Отображение рекламы утром или вечером.
- Использовать синий фон с белым текстом или черный фон с желтым текстом.
- Отображение рекламы только людям в городской области или людям в загородной области.
-
В клиническом исследовании больных раком для выявления необходимой концентрации лекарства для химиотерапии исследователи варьируют:
- тип лекарства: А или В;
- недельная доза лекарства: 5 единиц/кг или 10 единиц/кг;
- частота применения: один раз в неделю или 3 раза в неделю.
Выберите все верные ответы.
- Тип лекарства - категориальный признак.
- Исследователи могли бы измерять количество пациентов, испытывающих побочные эффекты (например, тошноту). Это было бы дополнительным фактором.
- Недельная доза лекарства - количественная переменная.
- Если бы исследователи варьировали дозу дополнительной терапии, это также было бы фактором.
- Недельная доза - категориальный фактор.
-
Бегун на короткие дистанции тренируется на трассе 200 м. Тренировки проходят регулярно: иногда утром, иногда вечером. Спортсменка решает варьировать разный тип обуви: с шипами и без. При беге она также варьирует положения рук: высокое или низкое. Выберите правильные варианты ответов:
- Спортсменка должна провести 6 (2+2+2) эксперимента для полнофакторного исследования.
- В ее исследовании используется 3 фактора.
- Ботинки с шипами могут быть отрицательным значением фактора, а без шипов - положительным.
- Измеряемым откликом системы будет тип обуви для бега.
-
При проведении полнофакторного эксперимента с 2 факторами и 2 уровнями варьирования была построена модель: \(\hat{y}=7+3x_A−4x_B+2x_Ax_B\). Факторами являются:
- А - поставщик сырья (низкий уровень - BASF, высокий уровень - DOW);
- B - температура плавления (низкий уровень \(320^o C\), высокий: \(340^o C\)).
Откликом системы является шероховатость поверхности произведенного пластика, который хотят минимизировать. Какова будет предсказанная моделью шероховатость для сырья от BASF при \(330^o\)?
-
Укажите сколько значащих цифр при следующей записи чисел: 3700, 0.0708, 2.540, 4.0, 0.80, 290.
-
Записать:
- результат сложения 2.3 и 1.26;
- результат сложения 507 и 1.2 в научной форме;
- результат умножения 2.65 на 1.9;
- результат возведения в степень \(35.3^2\).
-
Если экспериментально требуется определить сколько процентов вещества содержит раствор: 13 или 12 %, с какой точностью (в значащих цифрах) надо взвешивать?
-
Приведите результат вычислений с учетом значащих цифр. Для какого варианта Вы бы наименее доверяли точности результата (с учетом того, что последняя значащая цифра любого числа в формуле содержит его абсолютную величину)?
- \(\frac{\frac{90.7 + 100.5}{62.42} + 5.04}{10.0}\\\)
- \(\frac{9.7 + 100.5}{100.42} \cdot 5.4\\\)
- \((115 + 0.059) \cdot 0.05\)
3. Сравнительные эксперименты. Статистическая практика
Мы рассмотрели наиболее важную часть настоящего курса - планирование эксперимента и анализ его результатов. Следующие два раздела будут посвящены более узкоспециализированным темам, которые являются областью статистики (раздел математики). Приведенные далее рассуждения и примеры будут нужны для понимания природы данных и степени достоверности полученных результатов. Без понимания основ статистического анализа невозможно работать в аналитической лаборатории и анализировать любые численные результаты. Эта и следующая части настоящей работы относятся скорее к области аналитики (с отсылками к аналитической химии) и в большей мере применимы для сравнения полученных результатов и оценки точности построенных моделей.
В настоящей главе "Сравнительные эксперименты. Статистическая практика" мы рассмотрим что же такое статистика, полученные нами результаты и как мы действительно можем сравнить их друг с другом.
Если говорить кратко, статистика - это наука о работе с данными (как числовыми, так и категориальными). Она обладает обширным математическим аппаратом и позволяет реально взглянуть на окружающие нас вещи, понять, что все в окружающем нас мире относительно и обладает измеримой достоверностью. Осознать это и принять статистику я считаю наиболее важной задачей любого ученого. Вы не сможете ее избежать).
По своей сути, все окружающие нас явления не являются постоянными и абсолютными. Даже проводя измерение одной и той же величины в одинаковых условиях мы получим немного отличающиеся значения. Шанс, получить то или иное значение называется вероятностью.
Понятие вероятности является ключевым понятием вообще для всего, что нас окружает. Особенно это значимо для науки и экспериментов. Любое явление и любой результат обладают вероятностью - возможностью возникновения того или иного события. И эта вероятность - измерима.
Проводя исследования, рассчитывая результат эксперимента или просто планируя свою деятельность, мы всегда работаем с вероятностью. Неважно насколько мы уверены в своем результате/поступке - он будет обладать вероятностными характеристиками. И одной из основных задач исследователя является установление вероятности с которой он получил те или иные результаты, расчет вероятности того, что эти результаты значимо или не значимо отличаются от предыдущих и т.д..
Все в окружающем нас мире работает по статистическим законам и представляет из себя вероятностные величины. Так давайте же познакомимся с реальным миром!
Примечание. Данный курс является вводным и многие понятия в нем сформулированы и доказаны "не строго" (с математической точки зрения), а так, чтобы вы могли их легче запомнить и использовать в повседневных научных исследованиях. Но если рассказанное вам понравится и будет полезным, прошу исследовать приведенную в конце курса литературу.
3.1 Некоторые вводные определения
Начнем мы наше знакомство с основных понятий статистики: генеральная совокупность (ГС) и выборка. Именно они являются основой дальнейшего изучения.
Генеральная совокупность - множество всех объектом (или значений измеряемых величин), в рамках которых мы хотели бы сделать тот или иной вывод (сравнить их с другой генеральной совокупностью, рассчитать истинное значение и т.д.). В нашем случае, это, например, все возможное количество измерений отклика системы при фиксированном значении факторов.
Для определения ГС хорошим подходом является задать себе вопрос: "на какое множество объектов вы бы хотели обобщить ваши результаты исследования?" - это и будет вашей генеральной совокупностью.
И все бы хорошо, но как правило, объем такого множества крайне большой и нельзя провести измерение/исследование всех объектов в нем. На этот случай надо специальным образом "взять" из ГС определенное количество объектов - выборку.
При таком подходе, мы можем исследовать выборку и обобщить наши результаты на генеральную совокупность (с определенной достоверностью).
Ключевым условием выборки является ее репрезентативность (представительность) - она должна быть как можно более точной моделью генеральной совокупности (отражала ее свойства). В основном, репрезентативность зависит от количества объектов в выборке и от способа получения данных объектов (помните, мы всегда готовили, что нужно рандомизировать проведение экспериментов? Только в этом случае полученные измерения, формирующие нашу выборку, будут представлять ГС). Для обеспечения репрезентативности существует несколько подходов:
- Простая случайная выборка (simple random sample) - элементы ГС выбраны случайным образом.
- Стратифицированная выборка (stratified sample) - элементы выборки берутся случайным образом из областей генеральной совокупности (страт). Сами области соответствуют каким-либо свойствам выборки (например пол участника, поставщик реагента и т.д.). Такой подход позволяет сохранить точное количественное распределение объектов с разными свойствами в ГС.
- Групповая выборка (cluster sample). ГС делится на кластеры, которые по свойствам похожи между собой. Часто используется для экономии ресурсов и времени при формировании выборок (значения можно отбирать случайным образом не из всей ГС, а только из некоторых кластеров).
Примечание. В данном разделе мы принимаем тот факт, что выборка всегда отбирается из генеральной совокупности, но это не значит что мы всегда знаем какая это ГС. Например, если мы проведем 5 измерений одной и той же величины в нашем эксперименте, то мы получим выборку из ГС всех возможных измерений при наших условиях. Все условия для формирования выборок остаются действующими. Но в случае, когда мы не знаем ничего о ГС, будет работать только 1 подход (случайный выбор). Это как раз та причина, по которой эксперименты должны проводиться в случайном порядке и варьирование любых параметров должно также быть максимально случайным (спланированным, но случайным).
Но из чего в принципе может состоять выборка и генеральная совокупность, что такое объекты? С точки зрения статистики это просто набор свойств (скорее даже просто набор чисел). Т.е. говоря объект, мы подразумеваем то или иное свойство (или совокупность свойств). Синонимом свойства является фактор. Проблема в том, что не все эти свойства мы можем измерить и учесть (отсюда и появляется погрешность, зачастую мы даже не догадываемся о каком-либо влиянии). Но измеримые свойства бывают 2 видов.
-
Количественные (numeric) - которые можем измерить в численном виде и сравнит друг с другом. Они в свою очередь делятся на:
-
непрерывные (могут принимать любое значение в промежутке, например рост);
-
дискретные (принимают только определенные значения, например число детей в семье).
-
Качественные (категориальные, номинативные, categorical) - это те или иные свойства, которые на попали в 1-ую категорию (например цвет, пол, место жительство и т.д.). Обычно используются для разделения на группы и кодируются цифрами (но за этими цифрами нет физического смысла, нельзя применить математические операции).
Примечание. Иногда выделяют еще и 3 группу - ранговые (которые мы не можем измерить, но можем сравнить друг с другом, например, финалисты марафона). В основном ранги используются для расчета некоторых статистических параметров, а в практике работы с данными и интерпретации результатов используются крайне редко.
Стоит держать в голове, что из количественных переменных можно получить ранговые или категориальные (которые потом использовать, например, как качественные переменные для разбиения выборки на группы).
Задача. Предложите формулу для перевода количественной переменной "рост испытуемого" в ранговую и в категориальную.
С основным понятиями мы познакомились. Самое время перейти непосредственно к статистике и ее определениям.
3.2 Меры представления значений выборки или генеральной совокупности
За этим сложным термином скрывается всего лишь способ представления информации о выборке в виде одного числа. Именно этим занимается так называемая "описательная" статистика. На самом деле таких числе несколько, но благодаря им, мы можем получить представление обо всех данных в выборке и более того, в ГС.
Допустим, мы определились с нашим экспериментом, выбрали генеральную совокупность, провели эксперимент несколько раз и подготовили выборку. И что теперь?
Самое первое, что имеет смысл сделать - построить распределение измеренных величин в зависимости от объекта выборки - гистограмму. Визуализация - ключевая стадия понимания любых данных. Вспомните, мы строили графики Пито - тоже гистограмму, чтобы наглядно оценить влияние факторов на результат. Здесь примерно тоже самое, но строим мы гистограмму частот - как часто встречается тот или иной признак для выборки (рис. 30).
|
|
Рис. 30. Гистограммы для количественных (a) и качественных (b) переменных. |
Код для генерации данных:
# Generate random normal disturbed numbers
x <- 50 + rnorm(200)
# Create Frequency Table Using the Random Numbers
h <- hist(x, breaks=20, plot=FALSE)
# Plot the Distribution, with its tails highlighted in a different color
plot(h, col=3, main='test normal data')
# Generate binary data
y <- rbinom(n=200, size=1, prob=0.3)
h2 <- hist(y, breaks=2, plot=FALSE)
plot(h2, col=4, main='test binary data')
И вот ведь удивительная штука, но если нет систематического воздействия на систему (т.е. все воздействия происходят случайным образом), то гистограмма численных свойств всегда будет иметь вид нормального распределения (как на рисунке 30 (a)). Это своего рода ключевое распределение для статистики. И важно всегда проверять действительно ли у вас получилось нормальное распределение, если хотите использовать стандартные способы описательной и сравнительной статистики.
Примечание. Как вы можете видеть, чем более сильно величина отклоняется от центра, тем реже встречаются такие значения. Или другими словами - тем меньше вероятность получить такое значение при проведении эксперимента.
Стоит помнить, что на практике мы можем получить распределение любого вида - все зависит от эксперимента и типа данных (можете поискать в интернете различные примеры распределений). Описательная статистика как раз и занимается нахождением величин, которые могут описать тип распределения.
3.2.1 Меры центральной тенденции
Если мы посмотрим на приведенные распределения данных и заходим описать их одним числом, то вероятно, это будет число, при котором у нас наибольшее количество результатов (т.е. центр). Сделать мы это можем 3 способами (меры центральной тенденции).
- Мода (mode) - значение измеряемого признака, которое встречается максимально часто.
- Медиана (median) - значение признака, которое делит упорядоченное множество данных пополам (или среднее двух центральных значений, если количество элементов четное).
- Среднее (mean - среднее арифметическое) - сумма всех значений признака, деленная на количество измерений. Для выборки используется обозначение с подчеркиванием сверху (\(\overline{x}\)), а для генеральной совокупности - \(\mu\).
На основании этих величин можно представить себе вид распределения и сравнить его с другими распределениями. Таким образом, у нас появилось первое конкретное число, с которым мы можем работать (описывать наш эксперимент и полученные результаты, а также сравнить их с прочими результатами).
Более того, описанные способы расчета центральной тенденции позволяют нам представить вид распределения (рис. 31).
|
Рис. 31. Пример распределений при разных значениях моды, медианы и среднего (взято с https://stats.stackexchange.com/). |
Выводы попробуйте сделать сами. Но основной вывод: "если распределение симметрично, унимодально и не имеет выбросов - можем использовать любой вид представления центра". И обычно это среднее (поскольку нормальное распределение встречается чаще всего, а среднее удобнее для математических расчетов и более информативно). Но всегда нужно проверять вид распределения, прежде чем использовать среднее как меру степени выраженности некоторого значения, иначе это может привести нас к неверным выводам (вот тут есть пару интересных примеров).
Задача. Подумайте, почему в среднем арифметическом значении содержится больше информации об объектах выборки. Для этого нужно вспомнить/найти/подумать над формулы расчета каждого из мер центральной тенденции.
В нашем случае мы ограничимся рассмотрением только среднего значения. Основные свойства среднего приведены ниже.
- \(M_{x+c} = M_x + c\). Если к каждому значению выборки прибавить константу, то среднее также увеличится на значение данной константы.
- \(M_{x \cdot c} = M_x \cdot c\). Аналогично 1-ому, но с умножением.
- \(\sum(x_i - M_x) = 0\). Сумма отклонений всех значений от среднего арифметического будет равна 0 (легко представить графически - т.к. среднее находиться посередине всех значений выборки).
Задача. Нарисуйте, как будет меняться вид распределения для 1-ого и 2-ого случая.
3.2.2 Меры изменчивости
Следующее, что приходит на ум при анализе распределения - ширина гистограммы или мера ее изменчивости. Вот некоторые примеры, как можно численно охарактеризовать данное свойство.
- Размах (range) - расстояние между максимальным и минимальным значением. \(R = X_{max} - X_{min}\). Несмотря на простоту, эта мера опирается только на 2 значения из всей выборки, что не очень представительно и информативно. К выбросам он не устойчив.
- Дисперсия (variance) или средне квадратичное отклонение - насколько в среднем наши значения отклоняются от среднего по выборке. \(D = \frac{\sum (x_i - \overline{x})^2}{N}\). Чтобы понять зачем нам тут нужен квадрат (избавились от отрицательных значений) - посмотрите на 3 свойство среднего. К тому же квадратичные функции гладкие и с ними очень удобно работать в математике. Однако квадрат величины не имеет для нас большого смысла - сложно сравнивать с реальными значениями.
- Стандартное отклонение (СО, standard deviation, STD) - корень из дисперсии: \(\sigma = \sqrt{D}\). Он показывает реальное среднее отклонение от среднего по выборке (в тех же единицах измерения). В основном используется именно СО.
При этом стандартное отклонение для выборки обозначается как \(sd\), а для ГС: \(\sigma\), и это неспроста. Дисперсии тоже отличаются: для выборки \(D = \frac{\sum (x_i - \overline{x})^2}{n - 1}\), для ГС: \(D = \frac{\sum (x_i - \overline{x})^2}{N}\). Число \(n\) в знаменателе называется числом степеней свободы, т.е. количество независимых переменных в выборке, и оно меньше на единицу чем в ГС. Это вызвано тем, что выборка зависит от ГС и ее показателей (формальное обоснование оставим за сценой). Ведь по сути само понятие выборки нам нужно, чтобы на основании малого количества данных представить, что происходит на самом деле в генеральной совокупности.
Примечание. Число степеней свободы - значимый параметр в статистике и он не раз нам еще понадобится. Строго говоря - это количество факторов (элементов информации), которые могут варьироваться (которые мы можем изменять), при расчете того или иного параметра (в случае со СО выборки мы не можем варьировать среднее, поскольку оно связано с ГС, поэтому из количества переменных, мы вычитаем 1 значение, которое "можно найти, вычитанием остальных независимых элементов из среднего").
Свойства дисперсии.
-
Не изменчивость формы распределения при добавлении константы:
- \(D_{x+c} = D_x\)
- \(sd_{x+c} = sd_x\)
-
Изменчивость данных увеличится при умножении данных на константу:
-
\(D_{x \cdot c} = D_x \cdot c^2\)
- \(sd_{x \cdot c} = sd_x \cdot c\)
Опять же - всегда рекомендую строить графические примеры, чтобы понять почему так происходит.
Вот собственно и все основные численные характеристики распределения величин в выборках. Далее мы будем рассматривать вытекающие из них свойства и параметры, которые широко применяются в экспериментальной практике. Однако заключительной числовой характеристикой распределения являются его квантили.
3.2.3 Квантили распределения
Квантили - значения признаков, которые делят упорядоченные данные выборки на равное число частей. И да, медиана это один из квантилей - половинный квантиль (делит выборку на 2 равные части). Еще один частый пример квантилей - квартили. Это значения (3 точки), которые делят упорядоченные данные выборки на 4 части. Находятся аналогично медиане для разбитых ее участков.
А нужны нам эти точки для того, чтобы охарактеризовать распределение визуально. Они позволяют построит очень распространенный в статистике график представления результатов - box plot (ящик с усами), рис 32.
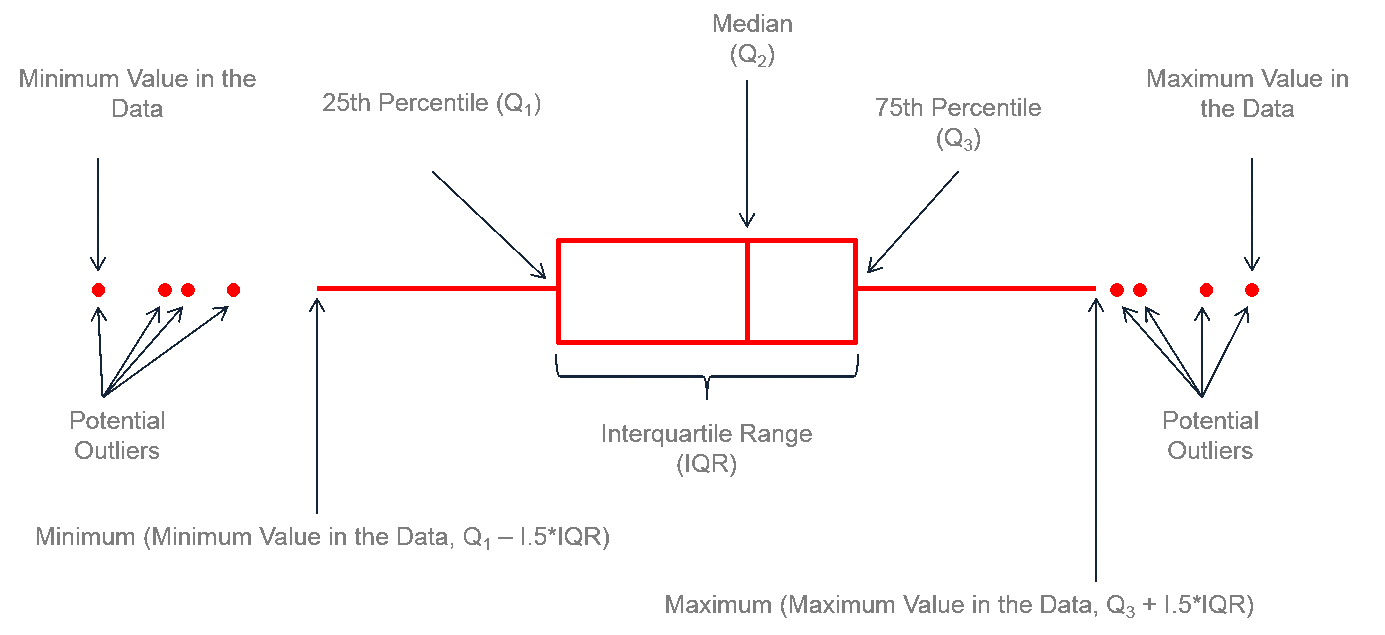
|
Рис. 32 (a). Анатомия box plot. |
|
Рис. 32 (b). Примеры box plot с сайта https://media.nature.com и соответствующие им распределения. |
С помощью данных графиком очень удобно сравнивать различные наборы экспериментальных данных. Вот пример кода на R для построения простого box plot:
# Generate random numbers
x <- 50 + rnorm(200)
# Boxplot
boxplot(x)
Поясним анатомию box plot. Линия внутри прямоугольника - медиана, верх и низ прямоугольника - 3 и 1 квартиль соответственно. Чем больше расстояние между 3 и 1 квартилем, тем больше вариативность нашего признака. При этом если медиана не по центр - распределение скошено. В свою очередь усы - это 1.5 межквартильных размаха (в них будет 50 % наблюдений). И если значения выходят за рамки этих усов, то они отображаются точками. Особо выбивающиеся значения стоит проверить на возможные выбросы.
Иногда усы на графике соответствуют максимальному и минимальному значению (другой способ отображения box plot, используется реже).
На этом действительно все с описанием распределений и время перейти к самой статистике. И основой ее являются нормальное распределение и центральная предельная теорема.
3.3 Статистика и сравнение данных
3.3.1 Нормальное распределение
Мы уже сталкивались с термином "нормальное распределение" и успели узнать, что это основное распределение в статистике. Большинство экспериментальных данных со случайной погрешностью подчиняется данному закону распределения (рис. 33). Но что значит распределение, помимо частотной гистограммы и числовых характеристик? В первую очередь - это закон, по которому распределяется вероятность получения тех или иных величин. Раз это закон, то существует выверенная математическая формула (формула Гаусса), согласно которой наши наблюдаемые значения отклоняются от среднего.
|
Рис. 33. Нормальное распределение. |
Примечание. Прошу вас ненадолго задуматься, что практически все величины в нашем мире подчиняются нормальному распределению. Это удивительно! И объяснимо.
Свойства нормального распределения:
- симметрично;
- унимодально.
Как уже отмечалось, поскольку распределение подчиняется строгому закону, мы можем рассчитать сколько наблюдений будет соответствовать тем или иным участкам гистограммы (наше распределение). Кроме того, мы сможем проводить и обратную операцию: определять вероятность получения того или иного значения эксперимента на основании его нормального распределения. Это позволит нам понять, стоит ли доверять полученному результату и насколько вероятно, что полученное значение (или сет значений) принадлежит той или иной системе (т.е. тому или иному распределению).
В частности, вероятность встретить значение, которое бы отклонилось от среднего на \(\pm 3 \sigma\) равняется 0.01 %, что очень маловероятно. Или другими словами 99 % наблюдений будут находиться в диапазоне \(\pm 3 \sigma\) (на графике это выражается соответствующей площадью под кривой).
С определением нормального распределения мы разобрались. Осталось понять как мы будем сравнивать различные распределения друг с другом, ведь несмотря на описательную статистику, измеряемые величины могут отличаться на порядки - на одной шкале их не представишь...
Для этого нам понадобиться стандартизация. Мы будем использовать так называемое Z-преобразование (Z-score). В результате такого преобразования мы получим Z-распределение, где среднее = 0, а стандартное отклонение = 1.
Приведения нашего нормального распределения к стандартному виду (Z-score) осуществляется по формуле:
Задача. Используя свойства среднего и дисперсии, рассчитайте новые характеристики полученного распределения и убедитесь, что они действительно равны 0 и 1.
При таком преобразовании форма распределения не изменится, а значит важную информации о нем мы не потеряем (если не используем дисперсию как признак).
Z - преобразование часто используется, чтобы все наблюдения перевести в z - шкалу (M = 0, sd = 1) для упрощения работы с данными. Однако процедура стандартизации часто используется и при расчете вероятности отклонения измеренного значения от среднего в единицах стандартного отклонения (запомните этот подход, он нам еще пригодится).
С использованием стандартизации, были установлены одни из широко используемых практических правил статистики: правила двух и трех сигм.
- \(M_x \pm \sigma \approx 68 \%\) наблюдений;
- \(M_x \pm 2\sigma \approx 95 \%\) наблюдений;
- \(M_x \pm 3\sigma \approx 100 \%\) наблюдений.
Однако Z-score позволяет нам рассчитать вероятность для любого отклонения, что позволит нам не использовать данные приближенные правила, а непосредственно рассчитывать вероятности появления того или иного значения.
Допустим среднее выборки \(\overline X = 150\), а стандартное отклонение \(sd = 8\). Какой процент наблюдений превосходит значение в 154 (рис. 34)?
|
Рис. 34. Пример расчета процента наблюдений. |
Для начала сделаем Z-преобразование для исследуемого значения: \(Z = \frac{154-150}{8} = 0.5\). После этого мы можем воспользоваться специальным сайтом и найти интересующий процент такого или еще более экстремального значения (рис. 34).
Ответ: 30.9 % наблюдений.
Примечание. Будьте аккуратны при использовании таблиц для работы с z-значениями: часто для интересующего нас z-значения указывается процент наблюдений, который не превосходит указанное z-значение.
Для нахождения вероятности и решения собственных задач используйте следующие ресурсы:
-
таблицы z-значений:
-
специальный сайт, позволяющим вычислить процент наблюдений в интересующем нас диапазоне (по умолчанию выставлено стандартное нормальное распределение M=0, sd=1).
-
Язык программирования R или Python (предлагаю самим найти в них соответствующие функции).
Примечание. При проведении ответственных вычислений используйте любые 2 источника, чтоб сверить свои ответы.
Примечание. Наиболее распространенные распределение непрерывных или псевдо-непрерывных величин:
- распределение Гаусса (нормальный закон распределения случайной величины, наиболее широко распространено);
- хи-квадрат (\(\chi^2\));
- распределение Фишера (\(F\));
- Распределение Стьюдента (\(t\)).
Наиболее распространенные распределения дискретных величин:
- Бернулли (бинарное);
- Пуассона.
Больше примеров и описаний можно найти здесь.
3.3.2 Центральная предельная теорема
Мы разобрались с характеристиками нормального распределения и как с ним работать. Действительно, наш мир - удивителен! И то, что нормальное распределение встречается в нем очень часто в любых проявлениях лишний раз подтверждает это утверждение. Но что действительно может "взорвать мозг", так это основа основ статистики - центральная предельная теорема (ЦПТ):
Распределение средних значений выборок одинакового размера из одной генеральной совокупности будет всегда стремиться к нормальному распределению! (при достаточно большом объеме выборки)
Более строгая формулировка теоремы выглядит примерно так:
где \(X\) - ГС исходной величины \(x\), с распределением \(F(x)\), \(X^n\) - множество из \(m\) выборок c размером \(n\), \(N\) - нормальное распределение, \(\mu_X\) - среднее ГС, \(D_X\) - дисперсия ГС.
Примечание. Математическая формулировку можно озвучить следующим образом. При многократном извлечении \(m\) выборок размером \(n\) из генеральной совокупности \(X\) с распределением \(F(x)\), средним \(\mu_X\) и дисперсией \(D_X\), распределение выборочных средних \(X^n = (X_1, X_2, ..., X_m)\) будет являться приблизительно нормальным со средним, равным среднему генеральной совокупности и с дисперсией, равной \(\frac{D_X}{n}\).
Поскольку мы чаще будем пользоваться величиной стандартного отклонения:
Полученная величина называется стандартной ошибкой среднего (standard error).
Суть ЦПТ в том, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, т.е. не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному!
И как частный случай, если мы будем извлекать выборки из генеральной совокупности (неважно с каким распределением, при очень большом количестве выборок) и рассчитывать для них средние, то они распределятся нормально относительно среднего генеральной совокупности. И отклонение от среднего будет тем меньше, чем больше размеры извлекаемых выборок (\(n\)) или чем меньше изменчивость исходного признака (\(\sigma_X\)).
Проверить это вы можете на сайте с соответствующей моделью.
Примечание. Теорема Ляпунова объясняет широкое распространение нормального закона распределения и поясняет механизм его образования. Теорема позволяет утверждать, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин (а наш мир так и устроен), дисперсии которых малы по сравнению с дисперсией суммы, закон распределения этой случайной величины оказывается практически нормальным законом распределения. А поскольку случайные величины всегда порождаются бесконечным количеством причин и чаще всего ни одна из них не имеет дисперсии, сравнимой с дисперсией самой случайной величины, то большинство встречающихся в практике случайных величин подчинено именно нормальному закону распределения.
Но самое приятное применение ЦПТ в том, что мы можем получить оценку истинного значения измеряемой величины по относительно небольшой выборке значений:
- среднее генеральной совокупности - приближенное истинное значение;
- среднее выборок - приближенное значение генеральной совокупности (по ЦПТ).
Таким образом, зная формулу распределения случайных величин в нормальном распределении и понимая, что все стремится к нормальному распределению (по ЦПТ), мы способны оценить насколько сильно новое измеренное значение отклонится от истинного (т.е. можем проводить измерения и сравнивать полученные результаты между собой действительно достоверно). На основании вероятности получить такое или еще более экстремальное значение, мы можем проводить статистическую проверку гипотез - основную операцию сравнения в статистике и выявлять статистически значимые различия.
Ограничивающим условием для ЦПТ в представленном виде является то, что в выборке должно быть более 30 значений, а сами выборки должны быть репрезентативны.
Пример. Используем на практике положения ЦПТ. Допустим, мы отобрали из генеральной совокупности только одну выборку размером 100 значений, характеристики выборки: среднее \(\overline{X} = 3\) и СО \(sd = 5\). Даже в таком случае мы можем оценить истинное значение через среднее всей генеральной совокупности, которое будет находиться в диапазоне среднего выборки со стандартной ошибкой среднего (мера изменчивости среднего):
$$ se = \frac{sd}{\sqrt{n}} = \frac{5}{\sqrt{100}} = 0.5 $$Истинное значение c 99% процентной вероятностью находится в диапазоне \(\overline{X} \pm 3\cdot se = 3 \pm 3 \cdot 0.5 = 3 \pm 1.5\). (см. правило 3 сигм). Более строгое обоснование будет дано далее.
Примечание. Если генеральная совокупность сильно отличается от нормального распределения, то чтобы получить нормальное распределение, хорошо описывающее распределение выборочного среднего, необходим размер выборки намного больше 30.
3.3.3 Доверительные интервалы
Говоря о ЦПТ мы уже немного коснулись сравнения данных. Однако для более строго понимания этого процесса необходимо понимать доверительные интервалы.
Мы уже рассмотрели пример, когда можно в определенной вероятностью предположить среднее ГС по одной выборки. И вы увидели, что в статистике (как и в реальном мире) нет абсолютных величин. Только интервалы и вероятность. Мы можем лишь оценить интервал, в который с определенной вероятностью попадет истинное значение - это и есть доверительный интервал среднего (для генеральной совокупности). А рассчитать такой интервал нам поможет ЦПТ и понятие квантилей с точки зрения стандартного Z-распределения.
Примечание. По своей сути Z-распределение показывает нам силу отклонения той или иной полученной величины от среднего в единицах стандартного отклонения выборки (внимательно изучите формулу для Z-score). А для оценки такого отклонения очень удобно использовать квантили, поскольку они делят шкалу распределения на равные отрезки относительно медианы (которая в случае нормального распределения совпадает со средним).
К настоящему моменту у нас на вооружение имеется 2 необходимых свойства:
- Согласно ЦПТ распределения выборочных средних СО будет равно \(se = \frac{sd_x}{\sqrt{n}}\).
- При этом из понятий о квантилях и Z-распределения мы можем рассчитать, какой процент наблюдений окажется в том или ином интервале от среднего ГС. Для упрощения воспользуемся правилом сигм и предположим, что 95% объектов будут находиться в диапазоне \(\mu \pm 1.96 se\).
Если взглянуть на это с другой стороны - со стороны выборочного среднего \(\overline{X}\), то c 95 % вероятностью оно находиться в интервале \(\mu \pm 1.96 se\). Это значит, что если бы мы взяли 100 выборок из ГС и рассчитали их средние, то для 95 выборок, эти средние также бы попали в данный интервал и если отложить от их среднего интервал \(\pm 1.96 se\), то он включили бы в себя среднее генеральной совокупности.
Примечание. Для лучшего восприятия возьмите листочек бумаги, нарисуйте распредлеение ГС, доверительный интервал для 95 % вероятности и убедитесь в сделанных предположениях (отложив соответствующие интервалы от выборочных средних и наблюдая, попадает ли в них среднее ГС).
Вот и ответ как нам использовать доверительные интервалы для оценки среднего ГС (нашего "реального значения"). Использовав обратный подход к рассуждению о доверительном интервале мы показали, что среднее ГС будет с той же вероятностью находиться в диапазоне \(\overline{X} \pm 1.96 se\), что и среднее выборки, находящееся в интервале \(\mu \pm 1.96 se\) (для такого доверительного интервала вероятность составит 95 %).
Пример. Рассчитаем доверительный интервал, для выборки с \(\overline{X} = 100\), \(sd = 4\), \(n=64\) в котором с 95 \% вероятностью находится среднее ГС.
Рассчитав такой интервал, мы можем быть на 95 % уверены, что он содержит в себе среднее генеральной совокупности (и предположительно, истинное значение). Это основная идея доверительных интервалов.
Примечание. Для большей уверенности мы могли бы использовать более широкий интервал, например \(\pm 2.58 se\) для 99 % вероятности.
3.3.4 Идея статистического вывода, р-уровень значимости
До сих пор мы работали по сути с результатами одного эксперимента. Настало время расширить горизонты.
Помимо представления об истинном результате, в экспериментальной практике нас интересует возможность сравнить результаты двух и более экспериментов (установить, действительно ли две выборки отличаются между собой).
Для статистически обоснованного ответа на такие вопросы нам потребуется разобрать идею статистического вывода. И сделаем мы это на примере.
Пример. Допустим, срок выздоровления пациентов при лекарстве А составляет в среднем 20 дней. Мы испытываем новое лекарство В и получили выборку со следующими характеристиками: \(N = 64\), \(\overline{X} = 18.5\), \(sd=4\). Действительно ли новое лекарство В работает лучше? Или мы получили просто допустимое отклонение от среднего одной ГС?
С одной стороны, среднее выборок отличается. Но мы теперь понимаем, что такой результат вполне мог быть получен случайно. Нам нужно оценить вероятность такого события и на основании полученных значений принять решение - отличается или нет.
В статистике для этого используется стандартный подход оценки статистических гипотез (названия гипотез всегда фиксированы).
- \(H_0\) - нулевая гипотеза. Всегда предполагает, что никакого воздействия нет. В нашем случае, предполагает, что новое средне принадлежат ГС (с \(\mu = 20\) дней).
- \(H_1\) - альтернативная гипотеза. Всегда предполагает, что нулевая гипотеза не верна (в нашем случае это то, что мы хотим доказать).
Решение:
Предположим, что верна нулевая гипотеза \(H_0\). Тогда, согласно ЦПТ, значение среднего исследуемой выборки (18.5) принадлежало бы ГС со средним 20 и ошибкой среднего \(se = \frac{sd}{\sqrt{n}} = \frac{4}{\sqrt{64}} = 0.5\). Тогда нам нужно ответить на вопрос насколько далеко отклонилось выборочное среднее 18.5 от среднего ГС 20, в единицах стандартного отклонения (ошибки среднего в данном случае) - для этого вспоминаем Z-распределение.
Это означает, что среднее выборки отклонилось от общего среднего на \(-3\) сигмы. Вероятность такого или еще более экстремального отклонения можно посмотреть из таблиц для z-преобразования, или воспользоваться этим сайтом. В нашем случае вероятность составит \(p = 0.003\), или 0.3 %.
В результате рассмотренного примера, мы установили, что 0 гипотеза верна с вероятность в 0.3 %. Тогда альтернативная гипотеза верна с вероятностью 99.7 %. Таким образом, мы можем отклонить нулевую гипотезу и завить, что наше лекарство действительно работает (но это не точно).
Величина достоверность 0 гипотезы (т.е. вероятность получить исследуемое значение как случайное отклонение от среднего ГС) обозначается как \(p\) и называется уровнем значимости. По своей сути это такой уровень вероятности, при котором можно получить такие, или еще более экстремальные значения. Считается, что при \(p < 0.05\) можно отклонять нулевую гипотезу и результат является статистически значимым (в некоторых случаях используют значение в 0.01).
Примечание. Существует понятие одностороннего и двустороннего p уровня значимости. Принято всегда рассматривать двусторонний уровень значимости, поскольку он позволяет дополнительно "застраховаться" от ложного результата (учитывает возможность отклонений в обе стороны). Однако, если сравниваемое значение физически не может существовать по другую сторону от среднего, тогда допускается использовать односторонний уровень значимости.
Расчет уровня значимости того или иного события, которое лежит в основе 0 статистической гипотезы является основой основ статистического анализа. Именно расчет уровня значимости для того или иного распределения (р-уровень значимости) лежит в основе различных статистических критериев, тестов и сравнений (поскольку p-уровень значимости является результатом этих действий). Благодаря этому показателю мы будем принимать те или иные статистические решения (отвергать или нет 0 гипотезу).
Обычно, нулевая гипотеза отклоняется, и различия считаются статистически достоверными, если p < 0,05. Однако часто в статистике используется более жесткий критерий достоверности различий (например, p < 0.01). Значение p-уровня значимости, которое выбирается, в качестве порога обозначается буквой \(\alpha\). Например, если исследователь решил, что \(\alpha = 0.05\), то и нулевая гипотеза будет отклоняться при условии, что p < 0,05. На протяжении курса мы будем отклонять нулевую гипотезу при условии, что p < 0,05 (кроме отдельно оговоренных случаев).
Примечание. Рекомендую ознакомиться с дополнительным материалом по р-уровню значимости: оригинал или интерпретация на русском.
Важно понимать, что любой статистический вывод подразумевает, что мы будем ошибаться. Существуют 2 типа ошибок:
- Ошибки I рода: отклонили 0 гипотезу, хотя она была верна (т.е. наш результат - случаен).
- Ошибки II рода: не отклонили 0 гипотезу, хотя была верна альтернативная.
Очень часто p-уровень значимости может выбираться чтобы минимизировать тот или иной вид ошибки.
Примечание. Использование доверительных интервалов зачастую рассматривают, как альтернативный способ проверки гипотез. В нашем случае, если значение 20 (предполагаемое среднее значение в генеральной совокупности) не будет принадлежать 95% доверительному интервалу, рассчитанному по выборочным данным, у нас будет достаточно оснований отклонить нулевую гипотезу. Проверьте, согласуются ли результаты двух этих подходов: рассчитайте 95% доверительный интервал для среднего значения, на примере с тестированием нового препарата.
3.3.5 Практика использования статистики для сравнения данных
Итак, мы разобрали с вами основные подходы к статистическому анализу данных и даже научились сравнивать среднее выборки и генеральной совокупности между собой.
Время разобрать несколько подводных камней, с которыми вы столкнетесь на практике, а также формальный подход к проведению сравнения выборок.
Первый закономерный вопрос: а что делать, если данных в нашей выборке меньше 30? Размер выборки очень важен, поскольку при недостатке значений ЦПТ перестает работать в том виде в котором мы ее изучили.
- Стандартное отклонение выборки уже плохо представляет СО генеральной совокупности.
- Средние значения наших выборок перестают формировать нормальное распределение.
Однако, сама форма распределения средних изменится не сильно. Оно продолжает быть симметричным и унимодальным колоколом. Но это распределение уже плохо описывается формулой Гаусса. Для него введено новое понятие - распределение Стьюдента" (t-распределение, рис. 35).
|
Рис. 35. t-распределение (Стьюдента). |
У такого распределения характерны более "высокие хвосты". Т.е. отклонения от среднего будут встречаться чаще. Именно такое распределение используется, когда число наблюдений в выборке невелико и/или \(\sigma\) (СО ГС) нам неизвестно (а это почти всегда). Обобщая сказанное: t-распределение используется всегда, когда есть сомнения в нормальности распределения ГС. Или проще - почти всегда нужно использовать t-распределение.
Поскольку данное распределение работает с малым количеством измерений, для него крайне важно понятие степеней свободы (\(df\)), которое зависит от наблюдений в выборке (\(n\)).
Чем больше количество степеней свободы (т.е. данных в выборке), тем больше t-распределение становиться похоже на нормальное. И это интересная особенность данного распределения - оно зависит от числа степеней свободы! Т.е. в отличие от жестко заданного нормального распределения (форма зависит только от \(\overline{X}\) и \(sd\)), для t-распределения вероятности встретить те или иные значения будут меняться в зависимости от количества данных в выборке (форма зависит от \(\overline{X}\), \(sd\) и \(df = n-1\)).
Т.е., по сути, при одинаковом с Z-критерием расчете:
р-уровень значимости для этого значения будет другой (чтобы рассчитать данный уровень нужно также воспользоваться таблицами или сайтом)
Примечание. Важно! До настоящего момента мы использовали упрощенное представление о распределении средних по ЦПТ. С определенным допущением мы полагали, что оно подчиняется нормальному распределения при выборках с более чем 30 значениями и отклонение от среднего в единицах СО рассчитывали как:
Строго говоря, это не так, поскольку в большинстве случаев нам не известна дисперсия ГС и сделать вывод о нормальности ГС мы не можем. В таком случае, мы обязаны всегда использовать t-распределение Стьюдента и рассчитывать p-уровень значимости для t критерия:
Для расчета вероятности получить такое отклонение случайно по t-распределению, нужно использовать специальные ресурсы.
Поэтому, правильнее будет сказать, что мы используем t - распределение не потому что у нас маленькие выборки, а потому что мы не знаем стандартное отклонение в генеральной совокупности. И в дальнейшем, на практике, мы всегда будем использовать t - распределение для проверки гипотез, если нам неизвестно стандартное отклонение в генеральной совокупности, необходимое для расчета стандартной ошибки (даже если объем выборки больше 30).
Пример. Время перейти к конкретным практическим примерам и посмотреть, как понимание ЦПТ и t-распредления поможет нам сравнить средние значения двух выборок с параметрами:
Подводный камень здесь заключается в том, что у нас нет ГС. Мы сравниваем 2 выборки из данной ГС. Поэтому для расчета нам понадобится так называемый парный t-тест (т.е. мы по сути проверяем, насколько сильно пересекаются доверительные интервалы исследуемых средних). Уже классический подход с гипотезами:
Допустим, верна 0 гипотеза. Тогда, при многократном повторении эксперимента мы бы извлекали по 2 выборки из одной ГС и величина:
При этом само распределение такой разности было бы t-распределением со средним = 0, а стандартное отклонение было бы равно:
т.е. вклад в общую ошибку среднего от средних 1 и 2 выборки был бы одинаков. Это разумно, поскольку мы предполагаем, что эти выборки принадлежат одной ГС.
При этом число степеней свобод для такого распределения будет равно:
что тоже весьма разумно, поскольку используются 2 выборки со своими степенями свободы.
Осталось рассчитать вероятность отклонения нашей разности, от предполагаемого 0 (аналогично расчету любого квантиля). Это и есть t-критерий:
Рассчитав соответствующее t-значение (т.е. насколько сильно отклоняется наш результат от предполагаемого среднего в единицах стандартного отклонения для t-распределения) и зная общее число степеней свободы, мы можем сравнить полученный результат с допустимым крайним значением (используем таблицы) или рассчитать p-уровень значимости для такого значения используя специальный сайт). Помним, что считаем вероятность получить такое отклонение в обе стороны!
Отметим, что при использовании критерия t-Cтьюдента необходимо учитывать соблюдение следующих требований:
- Гомогенности дисперсий. Дисперсии сравниваемых выборок должны быть приблизительно одинаковы (иначе наше допущение об их равном вкладе не имеет смысла). Для проверки данного требования используются критерий Ильина или критерий Фишера.
- При маленьком размере выборки (меньше 30) важно, чтобы распределение внутри выборки было нормальным (иначе не факт, что будет соблюдаться ЦПТ).
3.3.6 Графическое сравнение распределений
Помимо приведенных расчетов, мы можем использовать и графическое сравнение данных. Зачастую это удобно когда данных много и нужны быстрые выводы (наглядно, но вероятность совершить ошибку выше).
В начале остановимся на общих правилах представления результатов в статистике (да и в любой науке в принципе, рис. 36).
- Всегда добавлять название (хотя бы в подписи к рисунку).
- Подписывать оси.
- Указывать меру изменчивости данных (другими словами - погрешность).
|
Рис. 36. Пример представления данных в виде гистограммы. |
# Load ggplot2
library(ggplot2)
# create dummy data
data <- data.frame(
name=letters[1:5],
value=sample(seq(4,15),5),
sd=c(1,0.2,3,2,4)
)
# Most basic error bar
ggplot(data) +
geom_bar( aes(x=name, y=value), stat="identity", fill="skyblue", alpha=0.7) +
geom_errorbar( aes(x=name, ymin=value-sd, ymax=value+sd), width=0.4, colour="orange", alpha=0.9, size=1.3)
Но признанным стандартом для статистики является box plot или его вариации (рис. 37).
|
Рис. 37. Пример представления данных в виде box plot. |
# prepare the data from build in dataset
ozone <- airquality$Ozone
temp <- airquality$Temp
# gererate normal distribution with same mean and sd
ozone_norm <- rnorm(200,mean=mean(ozone, na.rm=TRUE), sd=sd(ozone, na.rm=TRUE))
temp_norm <- rnorm(200,mean=mean(temp, na.rm=TRUE), sd=sd(temp, na.rm=TRUE))
# You can read about them in the help section ?boxplot.
# Some of the frequently used ones are, main-to give the title, xlab and ylab-to provide labels for the axes, col to define color etc.
# Additionally, with the argument horizontal = TRUE we can plot it horizontally and with notch = TRUE we can add a notch to the box.
boxplot(ozone, ozone_norm, temp, temp_norm,
main = "Multiple boxplots for comparision",
at = c(1,2,4,5),
names = c("ozone", "normal", "temp", "normal"),
las = 2,
col = c("orange","red"),
border = "brown",
horizontal = TRUE
)
Лично мне нравится обозначать на графике box plot доверительный интервал и среднее (рис. 38).
|
Рис. 38. Пример представления данных в виде box plot со средним и доверительным интервалом для нормализованных данных. |
# scale the data
ozone <- scale(airquality$Ozone)
temp <- scale(airquality$Temp)
# drop NA values
ozone <- ozone[complete.cases(ozone), ]
temp <- temp[complete.cases(temp), ]
# calculate statistics
n_o=length(ozone)
mm_o=mean(ozone)
dd_o=sd(ozone)
error_o <- qnorm(0.950)*dd_o/sqrt(n_o)
n_t=length(temp)
mm_t=mean(temp)
dd_t=sd(temp)
error_t <- qnorm(0.950)*dd_t/sqrt(n_t)
# calculate confidence interval
inf_o <- mm_o - error_o
sup_o <- mm_o + error_o
inf_t <- mm_t - error_t
sup_t <- mm_t + error_t
# draw boxplot
boxplot(ozone, temp,
main = "Multiple boxplots with conf.int.",
at = c(1,2),
names = c("ozone", "temp"),
las = 2,
# col = c("orange","red"),
border = "brown"
)
# draw mean and CI
lines(c(0.75,1.25), c(inf_o, inf_o), col=4)
lines(c(0.75,1.25), c(mm_o, mm_o), col=2, lwd=2)
lines(c(0.75,1.25), c(sup_o, sup_o), col=4)
lines(c(1.75,2.25), c(inf_t, inf_t), col=4)
lines(c(1.75,2.25), c(mm_t, mm_t), col=2, lwd=2)
lines(c(1.75,2.25), c(sup_t, sup_t), col=4)
legend("topleft", c("95% CI", "Mean"), lty=1, col = c(4, 2),bty ="n")
Анализируя подобные графики можно составить мнение об изменчивости данных и об их различии. Вы уже убедились, что именно на основе информации о распределении, можно провести сравнение полученных результатов. Особенно это полезно в случае доверительных интервалов - если средние в данные интервалы не попадают (одно в интервал другого), то можно уверенно сказать, что выборки значимо отличаются.
3.3.7 Проверка данных на нормальность
Проверка экспериментально полученных данных на соответствие нормальному распределению очень часто встречается в статистических задачах (мы уже сталкивались с вами с таким требованием при разборе t-теста). Это необходимо, чтобы мы могли работать с арифметическим средним как с мерой центральной тенденции (иначе мы не сможем использовать изученные ранее подходы).
Один из самых простых способов проверки - просто построить гистограмму частот и сравнить ее вид с нормальным распределением при том же среднем и дисперсии. Однако, у такого подхода есть существенный недостаток - у нас нет числового критерия, а значит мы не можем доверять нашим выводам.
Другой способ - сравнить p-уровни значимости (или соответствующие им квантили) для полученного экспериментально распределения и для нормального распределения с такими же параметрами (средним и СО). Такой график называется квантиль-квантиль графиком (qq plot, рис. 39). Особенно это удобно, когда в выборках мало данных и мы можем отобразить на графике каждое из них.
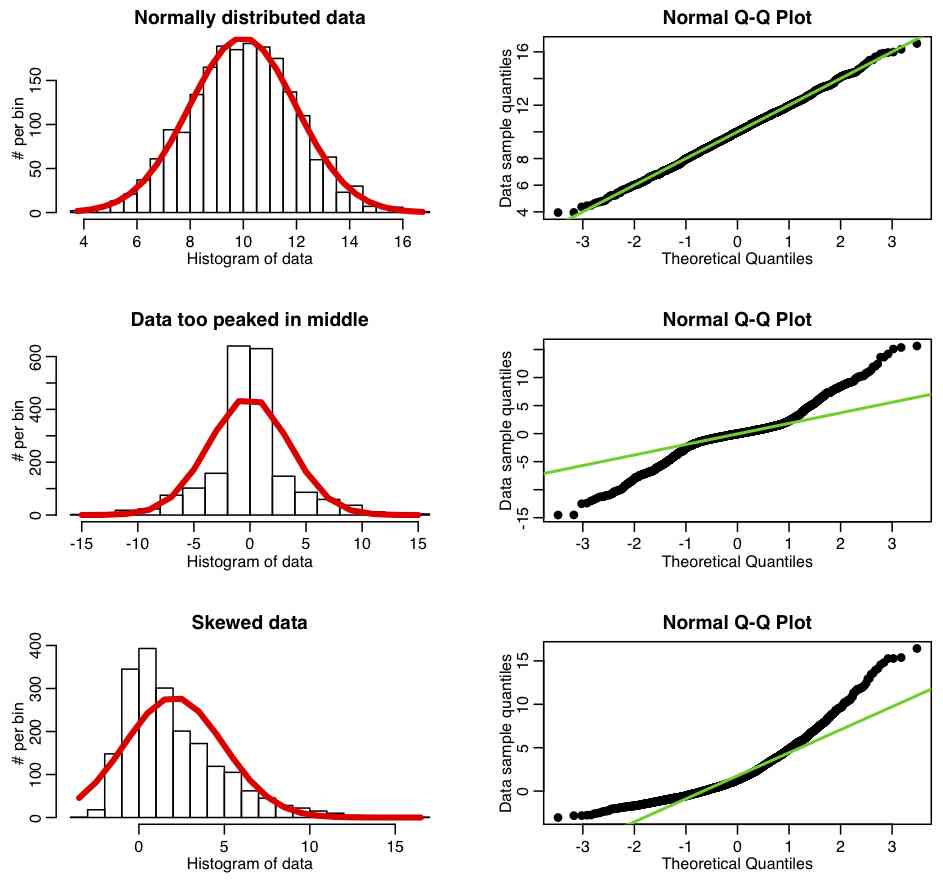
|
Рис. 39. Пример проверки на нормальность с помощью qq plot (больше примеров вы можете найти в интернете по запросу "qq plot with distribution example") |
Вы можете построить данный график сами в MS Excel. В приведенной ссылке дано немного некорректное приближение для квантиля, но хорошее описание процедуры построения графика. Для более корректного приближенного расчета квантиля из ранга переменной используйте формулу: \(\alpha = \frac{r - 1}{n - 1}\) (где \(\alpha\) - квантиль в долях от 1, \(r\) - ранг экспериментального значения в выборке, \(n\) - общее количество значений.).
Примечание. Чтобы исключить путаницу, разберем процедуру построения qq plot:
- Записываете все полученные данные для вашей выборки.
- Упорядочиваете их по возрастанию.
- Считаете для каждого значения его ранг (т.е. порядковый номер в зависимости от значения).
- Используете ранг, чтобы вычислить квантиль в долях единицы для каждого значения (мы не будем вдаваться в подробности, но \(\alpha\) - квантиль равен такому числу из распределения, что любая случайно взятая из выборки величина попадает левее этого числа с вероятностью \(\le \alpha\)). По сути ранг это и есть квантиль, поскольку ранг величины показывает насколько она сдвинута в распределении влево или вправо. Но чтобы получить квантиль, нужно абсолютное значение ранга перевести в относительную величину. Для этого нужно вычесть из ранга 1 (поскольку \(\alpha \in [0, 1]\) и разделить все на общее количество значений - 1 (для нормировки самого высокого ранга на 100 %). Таким образом, \(\alpha = \frac{r - 1}{n - 1}\).
- Используя полученные значения квантилей рассчитать значение, соответствующие Z-распределению для данного квантиля.
- Построить точечный график (scatterplot) "значения Z-распределения VS значения выборки" для каждого конкретного квантиля.
Таким образом, данные по оси 0Y соответствуют значениям экспериментального распределения без стандартизации (хотя можно встретить и стандартизованное представление). Данные по оси 0X соответствуют значениям стандартизованного нормального распределения (Z-распределения) с такими же средним и дисперсией. И каждое из данных по осям соответствует своему квантилю.
Интерпретировать график qq plot можно следующим образом:
- Если точки находятся на прямой линии под \(45^o\) (соответствует сравнению нормального распределения с нормальным), то наше распределение полностью соответствует нормальному.
- Если точки выше или ниже линии - частота экспериментальных данных больше или меньше, чем у нормального распределения для данного квантиля (часть гистограммы будет выше или ниже, чем у нормального распределения в данной области, рис. 39 - обращайте внимание на знак значений для вашего распределения и Z-распределения).
- 0 на 0X qq-plot означает среднее значение и медиану (совпадают для Z-распределения).
Пример кода на R. Рекомендую запустить и изучить как t-распределение отличается от нормального
# random t-distribution data
x <- rt(100, df=4) + 20
# qq plot with comparison line
qqnorm(x, pch = 1, frame = FALSE)
qqline(x, col = "steelblue", lwd = 2)
Еще одно важное применение графического подхода - проверка на выбросы.
Выброс - это явно отклоняющееся значение, которое не принадлежит исследуемой выборке, но почему-то включено в нее (обычно экстремально большое или маленькое). Обычно, выбросы появляются вследствие человеческого фактора или грубой ошибке в эксперименте (например, забыли нагреть).
Такие значения нужно убирать из расчетов, иначе формулы начнут работать неверно (ведь они основаны на среднем значении, а оно очень чувствительно к выбросам).
Третьим способом проверки на нормальность распределения является специальные тесты (считаются более достоверными, чем графический способ):
- Шапиро-Вилка;
- Колмогорова-Смирнова.
Они также работают по принципу расчета р-уровня значимости и проверки статистических гипотез (0-ая - исследуемое распределение не отличается от нормального, альтернативная - отличается). Это как раз тот редкий случай, когда полученный маленький р-уровень значимости сообщает нам плохую новость (что исследуемое распределение значимо отличается от нормального).
В любом статистическом пакете (включая MS Exel или RStudio) эти тесты уже реализованы. Можете смело их применять и сравнивать полученный р-уровень значимости с выбранным вами критическим значением (например, 0.05).
Если же мы получили свидетельство того, что наше распределение значимо отличается от нормального, то сравнить средние мы все еще можем, но уже по другому критерию: критерию Манна-Уитни (Whitney U-test). Этот критерий переводит все наши данные в ранговую шкалу (как при расчете медианы) и сравнивает уже не средние, а средние ранги (по сути мы используем медиану для оценки, а не среднее). Такой критерий гораздо менее чувствителен к наличию отклонений от нормальности и к выбросам. Но он менее точен, чем t-критерий для нормальных распределений. Предлагаю вам самим поискать в интернете как применять эти тесты, поскольку в экспериментальной и лабораторной практике встречаться с ними вы будете крайне редко.
3.3.8 Анализ выборок
Помимо простого сравнения двух средних (с помощью t-критерия), часто необходимо провести анализ нескольких выборок. Просто применять попарное сравнением с помощью t-теста будет неверно, поскольку это приведет к так называемому эффекту множественных сравнений (но об этом мы поговорим позже).
В случае анализа 3 и более выборок мы должны применять дисперсионный анализ. В рамках этого курса мы разберем простейший случай однофакторного дисперсионного анализа, чтобы понять как он работает.
Довольно часто в практических задачах выборки для сравнения получаются при исследовании какого-либо категориального признака. Например, мы исследуем гранулометрический состав 3 типов промышленно производимых удобрений и пытаемся понять, влияет ли фактор типа удобрения на процент фракции менее 2 мм. Та переменная, которая будет разделять наши объекты на выборки (категориальная переменная с нескольким градациями) называется независимой переменной. А та количественная переменная, по которой мы сравниваем выборки, называется зависимая переменная. Другими словами мы сравниваем несколько распределений в зависимости от одного категориального фактора.
Допустим, у нас есть три группы измерений:
Сформулируем гипотезы:
Примечание. Математическая запись \(!H_0\) говорит о том, что мы отрицаем нулевую гипотезу, т.е. хотя бы два средних из 3 не равны между собой (но мы ничего не говорим о том, какие это средние и т.д.). Обратите внимание, что 0 гипотеза говорит о средних ГС, т.е. предполагает, что все 3 выборки принадлежат одной ГС.
Для решения задачи, предположим, что верна 0 гипотеза. Тогда мы можем найти общее среднее для всех групп:
и общую сумму квадратов (характеризует насколько высока изменчивость наших данных без учета разделения их на группы, Square Sum Total):
Общее количество степеней свободы (исходя из предположения, что это одна выборка) составит:
Время задуматься из чего состоит общая изменчивость наших данных. Это всего 2 слагаемых.
- Межгрупповые изменчивость и степень свободы, т.е. насколько сильно значения разнесены друг от друга если сравнивать между группами (Square Sum Between).
где \(m\) - номер группы, \(c\) - количество групп.
- Внутригрупповые изменчивость и степени свободы, т.е. насколько сильно значения разнесены внутри групп (Square Sum Within).
где \(N\) - количество данных во всех 3 группах, \(m\) - номер группы, \(c\) - количество групп, \(n\) - количество данных в одной группе.
Проанализируем рассчитанные результаты. Общегрупповая изменчивость \(SST = SSB + SSW = 24 + 6 = 30\) и основная ее часть обусловлена межгрупповой изменчивостью. Можно предположить, что наши группы значительно различаются.
Рассчитаем формальный показатель, который позволит нам получить вероятность такого вывода: F критерий.
Задача. Интерпретируйте значение F критерия на основании приведенной формулы.
Теперь нужно рассчитать вероятность такого события и подтвердить / опровергнуть 0 гипотезу. Если верна 0 гипотеза и наши выборки берутся из одного распределения, то их средние отличались бы от среднего ГС (а значит и друг от друга) случайно и крайне не значительно (согласно ЦПТ). При этом внутри выборок была бы своя изменчивость, которая больше в \(\sqrt{n}\) раз, чем изменчивость между средними (согласно все той же ЦПТ).
Другими словами, \(F\) критерий был бы меньше 1, а распределение (названное F-распределением или распределением Фишера) имело форму, представленную на рис. 40.
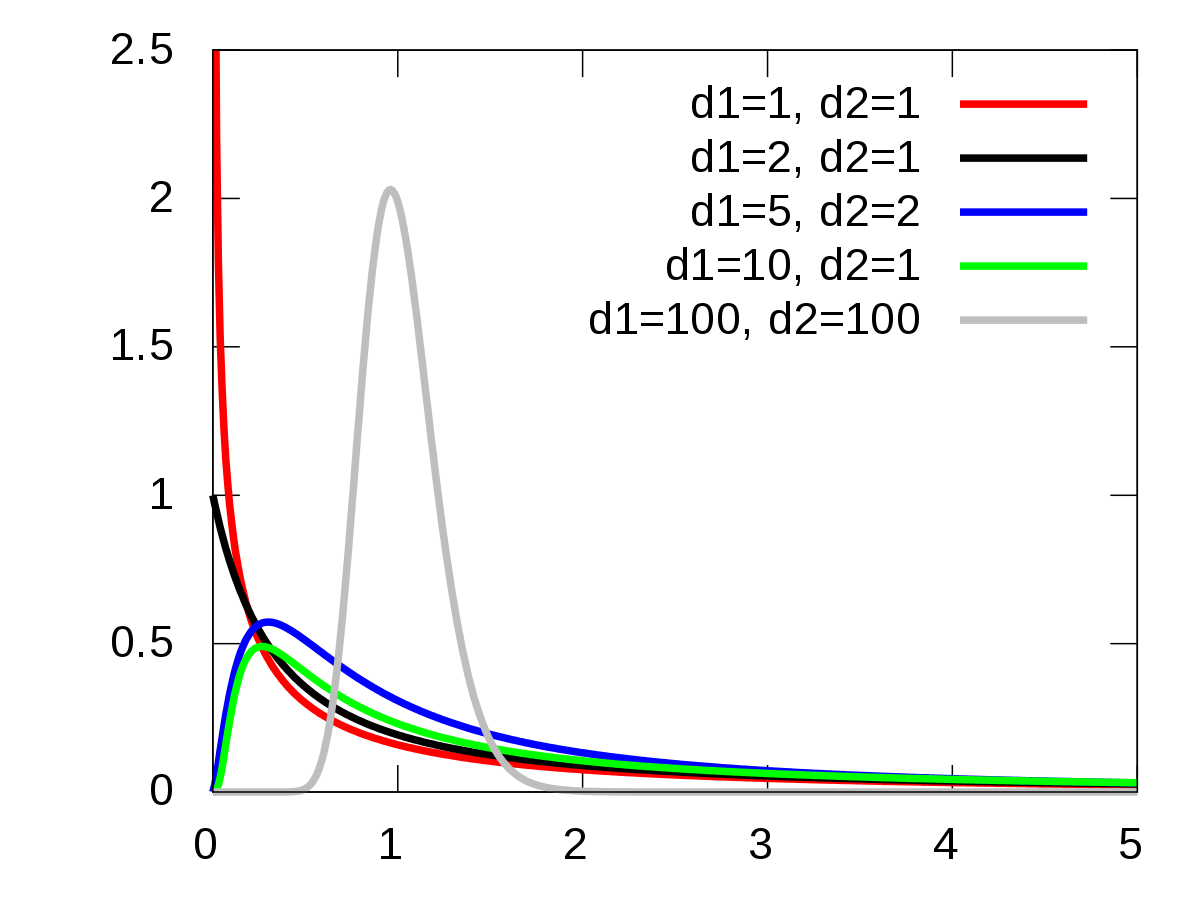
|
Рис. 40. F-распределение (изображение взято с en.wikipedia.org) |
Примечание. Такая форма распределения вызвана тем, что большинство F-значений при соблюдении 0 гипотезы были бы очень маленькими.
Для нашего значения в 12 единиц, мы можем рассчитать вероятность по F-распределению аналогично предыдущим задачам с t-критерием. Используем таблицу или сайт с распределением.
Если вы воспользуетесь сайтом, то обратите внимание, что там используют одностороннее распределение, поскольку F не может принимать отрицательные значения (т.е. двусторонний критерий физически не существует).
И ответ. Вероятность получить отклонение в 12 единиц или более составляет 0.008, что значительно меньше порогового значения доверительной вероятности в \(p=0.05\), а значит 0-ую гипотезу можно отклонить.
Примечание. Немного об обозначениях в дисперсионном анализе. Когда мы делим значение межгрупповой суммы квадратов на соответствующее число степеней свободы (число групп минус один), мы тем самым усредняем полученный показатель. Усредненное значение межгрупповой суммы квадратов называется межгрупповым средним квадратом.
Отношение внутригрупповой суммы квадратов к соответствующему числу степеней свободы (число всех наблюдений минус число групп) — это внутригрупповой средний квадрат
Поэтому формула F-значения (F-отношение) часто записывается как:
Примечание. По своей сути дисперсионный анализ делает ту же работу, что и t-критерий - сравнивает 2 выборки с точки зрения их средних. Но его преимуществом является то, что сравнивать мы можем сразу несколько групп и как вы увидите далее, не только по одному фактору.
3.3.9 Множественное сравнение
Мы уже разобрали 2 основных критерия сравнений выборок: t и F критерии. И казалось бы, они выполняют одну и ту же работу: сравнивают выборки. Почему же нельзя использовать просто попарное сравнение и ограничиться этим? Поскольку такой подход вызовет эффект множественного сравнения. Именно по этой причине мы не можем взять t-критерий и начать просто сравнивать результаты (по парно).
Давайте смоделируем ситуацию, когда у нас есть генеральная совокупность и мы случайным образом извлекаем из нее выборки и попарно сравниваем их средние между собой.
false_alarm1 <- function(m, n, a) {
# Создаем пустой дата фрейм с n наблюдениями (строками) и m выборками (столбцами)
d <- data.frame(matrix(0, n, m))
# Создаем матрицу возможных сочетаний переменных для будущего t-теста
s <- combn(1:m, 2)
# Создаем вектор с длинной 1000 для последующей записи 1000 извлечений выборок
x <- vector("numeric", 1000)
# Создаем собственную упрощенную версию t теста, которая возвращает только
# p value (значительно ускоряет всю функцию), но можете воспользоваться и встроенной функцией
t_test_pval <- function(x, y) {
se <- sqrt((var(x) + var(y))/n)
t_stat <- (mean(x) - mean(y))/se
df <- n + n - 2
pval <- 2*pt(abs(t_stat), df, lower.tail = F)
pval
}
for (q in 1:1000) {
d <- data.frame(apply(d, 2, function(i) rnorm(n)))
# Заполняем пустой дата фрейм случайными выборками,
# т.е. извлекаем из г.с. m-выборок
for (i in 1:ncol(s)) {
TEST <- t_test_pval(d[, s[1, i]], d[, s[2, i]])
if(TEST < a) x[q] <- 1
if(TEST < a) break
}
}
x <- as.data.frame(table(x))
barplot(x$Freq, names.arg = c("No", "Yes"),
col = c("Red", "Blue"),
main = x$Freq[2]/1000*100,
ylab = "Quantity",
xlab = "significant differences",
ylim = c(0,1000))
}
false_alarm1(2, 20, 0.05)
В результате 1000 кратного извлечения по 2 выборки из одной ГС при попарном сравнении средних мы получаем статистически значимое различие между 2 выборками из одной ГС в \(\approx 5 %\) случаях совершенно случайно! И это при малом количестве извлекаемых выборок. Для 8 выборок потребуется произвести по \(\frac{8 * (8-1)}{2} = 28\) сравнений. И если мы проведем эксперимент с попарным сравнением, то мы получим ложное статистически значимое различие уже в \(\approx 52 %\) случаев! Проверьте это с помощью кода.
И чем больше попарных сравнений, тем больше ложных срабатываний!
Происходит это по тому, что чем больше попарных сравнений, тем больше шанс ошибиться. И тогда для каждого извлечения выборок с их попарным сравнением хотя бы одна ошибка, но произойдет, что приведет нас к ложному выводу для всей совокупности выборок.
Таким образом вредный совет: если вы ходите получить значимое различие - проведите один и тот же эксперимент 1000 раз и вы получите хотя бы одно значимое различие между данными разных подходов (рис. 41)...

|
Рис. 41. Пример эффекта множественного сравнения с https://xkcd.com. |
Таким образом, при множественном сравнении нам необходимо корректировать порог р-уровня значимости, при котором мы принимаем решения. Это важно не только при попарном сравнении, но и в случае дисперсионного анализа при исследовании разных категориальных факторов. Поправки на множественное сравнение можно ввести разными путями.
- Поправка Бонферони (популярная, но ее никто не любит) - предлагает пропорционально корректировать уровень значимости \(\alpha\), при котором мы отвергаем 0 гипотезу пропорционально количеству парных сравнений \(\alpha = \frac{\alpha}{n}\). Но проблема в том, что она очень грубая и мы можем очень сильно снизить порог отклонения 0 гипотезы (т.е. упустить реальные открытия).
- Поправка Тьюки (Tukey HSD) - модифицирует t-критерий.
- False Discovery Rate, etc.
Не стоит забывать и о ключевом приеме - грамотной обработке данных и планировании эксперимента. Нужно в 1-ую очередь правильно формулировать гипотезу и повторять сравнительные эксперименты для нее. Если она верна, то в большинстве случаем, вы найдете различия.
Более подробно о различных поправках предлагаю Вам посмотреть самим. Также за бортом осталась тема многофакторного сравнения и ANalysis Of VAriance (ANOVA), которая является логическим продолжением нашего подхода (неплохо написано в wiki). Если вам интересны эти темы и статистика в целом, предлагаю начать самостоятельное ознакомление с этих курсов на stepic.org:
3.4 Вопросы по разделу
- Если мы провели исследование с целью выявить уровень знаний в области планирования эксперимента на 100 студентах кафедры химических технологий ЧГУ, то на какую совокупность мы можем распространить наши выводы?
- Если объем выборки достаточно велик (больше 100), то является ли такая выборка репрезентативной.
- Предположим, после лекции по статистике, один студент решил выяснить, как хорошо студенты психологического факультета разбираются в этом предмете. Он подготовил серию заданий и пригласил 30 своих друзей с факультета принять участие в тестировании. Исследователь утверждает, что он сформировал простую случайную выборку. Так ли это?
- В каких случаях вместо среднего значения лучше использовать моду или медиану в качестве центральной тенденции?
-
Укажите, в какой из выборок наибольшее стандартное отклонение (задание решить без расчетов):
- 1 3 2 4 5 7 1 8
- 100 300 250 400 230 280 320 112
- 15 10 13 7 28 31 20 32
-
Как соотносятся дисперсии двух выборок (постарайтесь решить данное задание не рассчитывая значения дисперсии, а ее свойствами):
- 1 3 5 6 6 7 9 11
- 5 7 9 10 10 11 13 15
-
Может ли стандартное отклонение принимать отрицательные значения?
- Соотнесите распределения и ящики с усами (рис. q-1).
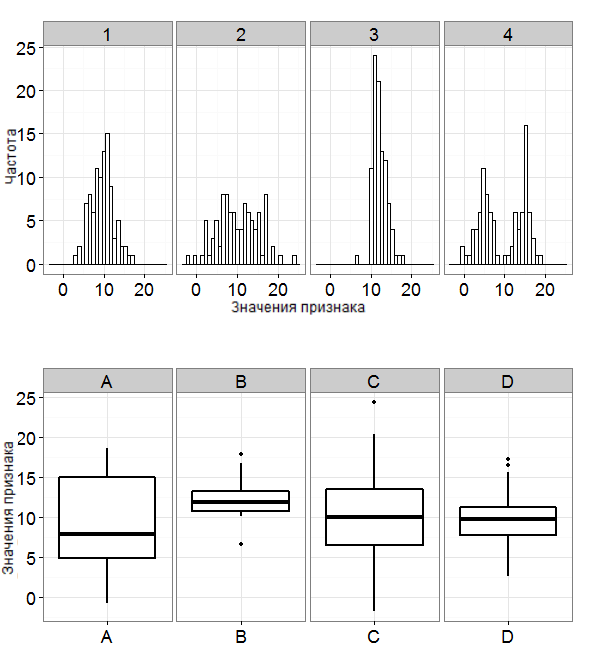
|
Рис. q-1. |
-
Если отдельное наблюдение в нашей выборке равняется 1000, при условии, что выборочное среднее равняется 10, то:
- такое наблюдение в принципе не может принадлежать выборке со средним значением равным 10, так как в 100 раз больше, чем выборочное среднее, а вероятность такого события стремится к нулю;
- можно рассматривать как необычное (выброс), т.к. оно очень далеко отклоняется от среднего значения;
- чтобы судить о том, насколько необычным является это наблюдение для выборки, необходимо знать, чему равняется стандартное отклонение.
-
Считается, что значение IQ (уровень интеллекта) у людей имеет нормальное распределение со средним значением равным 100 и стандартным отклонением равным 15 (M = 100, sd = 15). Приблизительно рассчитайте какой процент людей обладает \(IQ \ge 125\)? А какой процент людей обладает \(70 \ge IQ \le 112\)?
- Рассчитайте стандартную ошибку среднего при N = 100, если выборочное среднее равняется 10, а дисперсия 4.
-
Если мы рассчитали 95% доверительный интервал для среднего значения, то какие из следующих утверждений являются верными?
- Мы можем быть на 95% уверены, что истинное среднее значение принадлежит рассчитанному доверительному интервалу.
- Истинное среднее значение точно принадлежит рассчитанному доверительному интервалу.
- Истинное среднее значение точно превышает нижнюю границу 95% доверительного интервала.
- Если многократно повторять эксперимент, для каждой выборки рассчитывать свой доверительный интервал, то в 95 % случаев истинное среднее будет находится внутри доверительного интервала.
- Если многократно повторять эксперимент, то 95 % выборочных средних значений будут принадлежать рассчитанному нами доверительному интервалу.
-
Рассчитайте 99% доверительный интервал для следующего примера: \(\bar{x}=10, sd=5, n=100\).
-
Выберете верные утверждения
- Чем меньше p уровень значимости, тем сильнее полученные различия.
- Если бы в исследовании мы получили p = 0.9, это означало бы, что верна нулевая гипотеза.
- Все утверждения неверны.
- Статистически значимый результат, всегда означает ценный и осмысленный результат.
- Если p уровень значимости равен 0.003, то вероятность того, что верна нулевая гипотеза (новый препарат не влияет на скорость выздоровления) также равняется 0.003.
-
Если в определенной ситуации весьма рискованно отклонить нулевую гипотезу, когда она на самом деле верна, то лучше использовать показатель \(\alpha\):
- 0.001,
- 0.05,
- 0.1,
- 0.5?
-
Для выборки в 15 наблюдений при помощи t-теста проверяется нулевая гипотеза, что \(\mu=10\). Рассчитанное t-значение = -2 (t = -2). Рассчитайте p-уровень значимости для такого события (можете использовать уже знакомый нам сайт, укажите в настройках, что вы работаете с t - распределением и выберите нужное число степеней свободы).
-
В первом эксперименте для сравнения двух средних \(\bar{X_{1}}=17, \bar{X_{2}}=16\) применялся t-критерий Стьюдента, и эти различия оказались значимы (p = 0.001). Во втором исследовании, также при помощи t - критерия, сравнивались два средних \(\bar{X_{1}}=17, \bar{X_{2}}=36\) и эти различия не значимы при p = 0.8. В чем может быть причина таких результатов?
- Возможно, во втором эксперименте больше объем выборок и меньше изменчивость исследуемого признака.
- Возможно, в первом эксперименте больше объем выборок и меньше изменчивость исследуемого признака.
- Ни размер выборки, ни изменчивость исследуемого признака не может быть причиной таких результатов.
-
Соотнесите распределения и qq-plot.
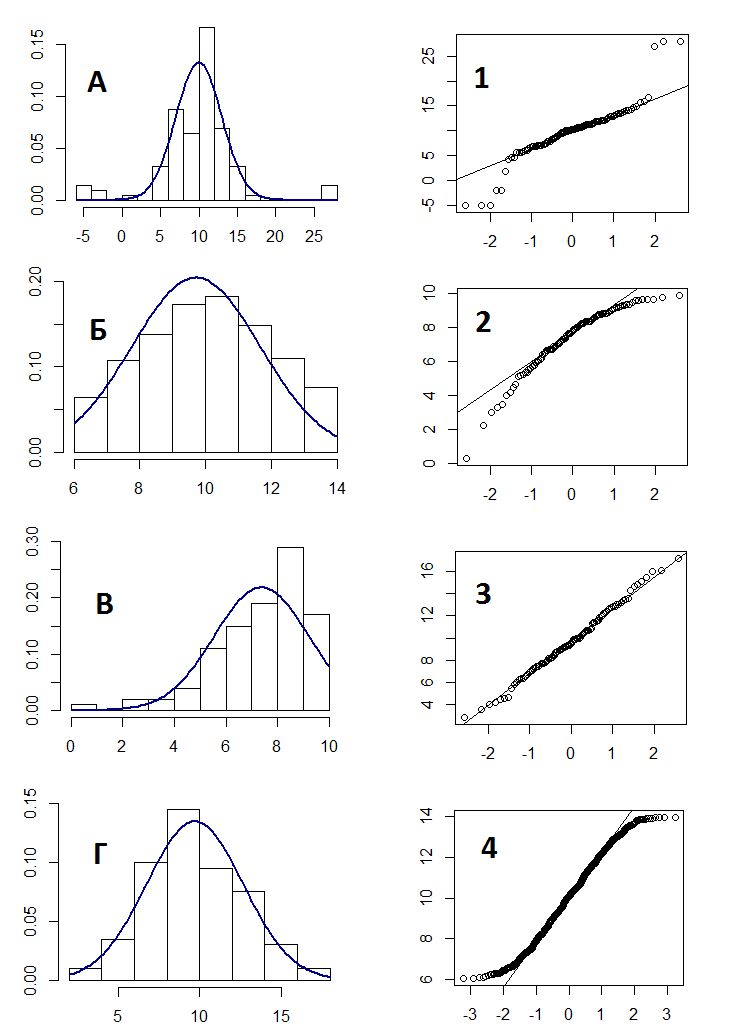
|
Рис. q-2. |
- Если для проверки нормальности распределения на выборке в 100 наблюдений мы применили Shapiro-Wilk test и получили p-уровень значимости, равный 0.001, то:
- распределение является бимодальным;
- распределение значимо отклоняется от нормального.
4. Построение точных моделей. Аналитическая практика
Пришло время заключительной части нашего курса - применение полученных знаний для построения точных моделей и градуировочных зависимостей, которые часто используются в аналитической химии. Однако для этого нам понадобится понимание новых тем статистического анализа: корреляции и регрессии.
4.1 Корреляция
Корреляция - степень взаимосвязи переменных. Насколько одна переменная статистически связана с другой. В нашем случае мы рассмотрим две переменный и разберемся что такое положительная и отрицательная корреляция и о чем нам может сказать коэффициент корреляции.
Надеюсь что смог вас убедить, что одним из самых простых способов что-либо понять является визуализация. Давайте рассмотрим следующие примеры взаимосвязи 2 величин (рис. 42).
|
Рис. 42. Примеры корреляции 2 величин (взято с сайта CQE Academy). |
На осях графика обычно откладывают значения соответствующих переменных и оценивают их вид взаимосвязи (как изменение одной переменной будет сказываться на изменении другой переменной).
Например, на подобном визуальном анализе взаимосвязей основан довольно широко используемый в анализе больших массивов данных метод попарного сравнения признаков (рис 43).
|
Рис. 43. Пример использования попарного сравнения признаков для 3 типов объектов в data science. |
Такой тип графиков называется диаграмма рассеяния (scetterplot) и многие статистические пакеты (включая R и MS Exel) обладают удобными механизмами их построения и показывают значения 2 переменных для каждого из исследованных объектов.
После того, как мы поняли и увидели корреляцию, нужно добавить объективности - ввести некий показатель, который оценивал бы в численном виде степень и вид взаимосвязи наших величин. И такой показатель есть - это коэффициент корреляции (\(r\)).
Давайте попробуем логически вывести данный коэффициент. Воспользуемся для этого связью 2 переменных (рис 44).
|
Рис. 44. Вывод коэффициента корреляции. |
Обозначим на графике средние 2 признаков. Наша диаграмма рассеивания разбилась на 4 области, которые обозначают тип взаимосвязи в зависимости от кодированного значения признака (положительная или отрицательная). Анализируя количество данных в каждом квадрате мы можем выяснить знак корреляции.
Следующий шаг - рассчитаем отклонение каждого значения от среднего, сложим и усредним эти отклонения с учетом степеней свобод:
Полученный показатель называется ковариацией.
Обратите внимание, что знак этого произведения будет зависеть от того, в каком из 4 квадратов находятся наши данные. В нашем случае большинство из рассчитанных отклонений положительные, поскольку большая часть точек находится в I или III квадрате.
Полученный параметр показывает нам силу и тип взаимосвязи переменных: чем он больше, тем сильнее связаны переменные, а знак ковариации показывает нам направление связи.
Осталось добавить последний штрих: сделать нашу ковариацию универсальной для сравнения различных величин. Для этого нужна нормировка (чтобы уйти от абсолютных величин). Полученную ковариацию нужно разделить на величину изменчивости обоих признаков, т.е. на их стандартные отклонения:
Задача. Как вы думаете, почему нужно уходить от абсолютных величин, чем это мешает нам в случае сравнения?
Таким образом мы получили коэффициент корреляции (или коэффициент корреляции Пирсона). Многие из вас знакомы с коэффициентом корреляции и представляли его слегка по другому, давайте произведем некоторые дополнительные вычисления:
Я думаю именно в таком виде вы могли быть знакомы с коэффициентом корреляции.
Посмотреть, как коэффициент корреляции влияет на связь величин вы можете на сайте.
На том же сайте приведена еще одна важная величина - коэффициент детерминации (или общей дисперсии, shared variance), который равен квадрату коэффициента корреляции и показывает какая часть изменчивости одной переменной может быть объяснена другой переменной (т.е. насколько сильно одна дисперсия зависит от другой): \(R^2 \in [0; 1]\). Более подробны мы рассмотрим его в случае линейной регрессии.
Пример. Давайте используем коэффициент корреляции для проверки статистических гипотез на примере случайно сгенерированных данных. Пусть
Обратите внимание - мы сформулировали двунаправленную альтернативную гипотезу (т.е. не говорим в какую сторону направлена зависимость, просто говорим, что ее нет и выборки не связаны).
Рассчитаем р-уровень значимости на основании t-критерия для \(dF = N-2\) степеней свобод (т.к. работаем с 2 переменными). Мы не будем подробно останавливаться на расчете, для него я рекомендую использовать специализированное ПО (в нашем случае RStudio):
N <- 50
x <- rnorm(n = N, mean = 0, sd = 1) # генерируем данные
y <- rnorm(n = N, mean = 0, sd = 1) # генерируем данные
plot(x, y, lwd=5)
cor.test(x, y)
Результатом будет примерно следующее (график изучите сами в RStudio):
data: x and y
t = 1.2265, df = 48, p-value = 0.226
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.1093331 0.4317197
sample estimates:
cor
0.1743197
Обратите внимание, что мы рассчитали коэффициент корреляции, t-статистику и р-уровень значимости для нее. На основании полученных данных нельзя отвергнуть 0 гипотезу, а значит данные действительно случайны (что и требовалось доказать).
Как вы думаете, если коэффициент корреляции равен 0,7, то такая взаимосвязь всегда будет статистически достоверна (p - уровень значимости обязательно будет меньше 0.05)?
Так вот нет. Высокая корреляция не обязательно означает статистически значимую взаимосвязь. Чтобы говорить о взаимосвязи, нужно иметь представление о степенях свободы (т.е. на скольких измерениях сделан подобный вывод). Если у нас df = 3, то есть, всего 5 наблюдений в каждой из выборок, то мы должны получить коэффициент корреляции, равный или больший, чем 0.98769, чтобы p-value стал меньше 0.05 и мы смогли утверждать о том, в ГС коэффициент корреляции не равен нулю (данные взяты из таблиц)! Того же вывода можно добиться изменяя число степеней свобод в коде R, приведенном выше. В любом случае, нам нужно рассчитывать р-уровень значимости и анализировать статистические гипотезы, чтобы быть уверенными в наличии взаимосвязи в ГС.
Примечание. Именно по этому в аналитической химии всегда требуются высокие коэффициенты корреляции. На основании малого количества данных (обычно 5 точек для градуировки) нам нужно сделать вывод обо всей генеральной совокупности (все возможные подобные эксперименты при данных условиях).
Условия применения коэффициента корреляции Пирсона.
Как и у любого другого статистического критерия, в нашем случае есть некоторые особенности и ограничения в применении критерия корреляции.
- Характер взаимосвязи данных должен быть линейный и монотонный (можете подробнее поискать определения данных слов в википедии). Возможно, для этого придется разбивать вашу выборки на отдельные диапазоны - подвыборки (частый прием в аналитической химии).
- Должны быть соблюдены следующие характеристики переменных: отсутствие выбросов и нормальность распределения (поскольку идея коэффициента корреляции связана со средним значением, а его представительность как центра очень чувствительна к этим условиям).
- Всегда помните: корреляция не доказывает причинно-следственную связь! Выявление такой связи - задача не метода, а экспериментатора. Никакой статистический метод не установит причины. Он лишь покажет как факторы связаны друг с другом и может подтвердить значимость различий, а выводы - делайте сами.
- Всегда помните о возможном наличии 3-ей переменной. Это такая переменна, которую мы не рассматриваем, но которая связана с 1 и 2 рассматриваемым признаком и обеспечивает их корреляцию (поищите в интернете "интересные корреляции" и подумайте, какая там может быть третья переменная. Или вот, статья на хабре).
Если с выполнением необходимых условий у нас проблемы, можем использовать некоторые непараметрические аналоги, например коэффициент корреляции Спирмана или тау Кендалла (переходят от реальных значений к ранжированным, т.е. к медиане, как мере центральной тенденции).
Коэффициент корреляции Спирмана:
где \(d\) - разность рангов.
Пример. Рассчитаем коэффициент корреляции Спирмана для следующих данных:
| X | Y | rank X | rank Y | d^2 |
|---|---|---|---|---|
| 3 | -1 | 1 | 1 | 0 |
| 5 | 4 | 2 | 4 | 4 |
| 7 | 4.5 | 3 | 5 | 4 |
| 9 | 8.5 | 4 | 7 | 9 |
| 10 | 12 | 5 | 10 | 25 |
| 11 | 8 | 6 | 6 | 0 |
| 11.5 | 9 | 7 | 9 | 4 |
| 12 | 9 | 8 | 8 | 0 |
| 14 | 18 | 9 | 12 | 9 |
| 17 | 17 | 10 | 11 | 1 |
| 30 | 1 | 11 | 2 | 81 |
| 32 | 2 | 12 | 3 | 81 |
Тогда \(r_s = 0.23\), при \(r = -0.1\), что все-таки лучше, чем ничего.
4.2 Регрессия с одной независимой переменной
Следующим шагом является построение линейной модели и оценка ее статистической значимости. Мы уже сталкивались с таким заданием при планировании и анализе эксперимента. Здесь мы приведем некоторые статистические особенности таких моделей и способа их построения. Для этого мы рассмотрим одномерный регрессионным анализ, который позволяет проверять гипотезы о взаимосвязи одной количественной зависимой переменной (отклик) и несколькими независимыми переменными (измеряемые значения). Но в нашем случае мы разберем самый простой и наиболее часто встречающийся вариант - простой линейной регрессией. С помощью этого метода можно исследовать взаимосвязь только двух переменных, но принцип работы и интерпретация результата будут аналогичны любой регрессии. Частным примером являются градиуровочные кривые (или уравнения связи) для аналитических методов (когда мы пытаемся найти концентрацию в зависимости от аналитического сигнала).
Вот несколько важных терминов:
- зависимая переменная (отклик, располагается на оси 0Y) - для которой ищем уравнение (т.е. пытаемся рассчитать ее из эксперимента).
- независимая переменная (фактор, предиктор, располагается на 0X) - та, которую измеряем в ходе эксперимента.
- линия регрессии - линия, отображающая направление взаимосвязи и описывающая распределение данных (т.е., чтобы каждая точка была максимально близко к нашей линии при прохождение ее через центр облака точек).
Давайте попробуем рассчитать положение интересующей нас линии, которая покажет нам взаимосвязь 2 переменных. Общее уравнение прямой:
где \(b_0\) - свободный член (intercept, отвечает за то место, где наша линия пересекает ось 0Y); \(b_1\) - наклон, чувствительность (slope, отвечает за направление линии (верх/низ) и угол наклона линии).
Примечание. Рекомендую вернуться к 1 части планирования эксперимента и соотнести модели экспериментов с материалом по линейной регрессии.
Для нахождения коэффициентов (параметры линейной регрессии) используется уже упоминавшийся метод наименьших квадратов (МНК). Из названия следует, что этот метод минимизирует сумму квадратов отклонений (остатков) каждой точки от прямой.

|
Рис. 44. Принцип работы МНК для построения линейной регрессии. |
Задача. Вспомните/подумайте почему мы используем квадрат остатков с точки зрения статистики?
Вывод формул мы оставим за кадров и напишем только конечные формулы для коэффициентов:
Задача. Проанализируйте коэффициенты с точки зрения входящих в них компонентов. Какой коэффициент и как отвечает за направление прямой и почему?
Таким образом, с использованием регрессии мы можем не только определить направление и силу взаимосвязи (это нам позволяет сделать и коэффициент корреляции), но и получить математическую модель, по которой потом будем строить предположения (\(\hat{y}\)) и сравнивать их с реальными данными (\(y\)).
Однако мы ведь все оцениваем критически, помните? Поэтому следующим логичным вопросом, после построения модели будет: "а на сколько статистически значимым будет взаимосвязь 2 наших величин?"
Как вы думаете, какой коэффициент отвечает за это? Правильно, \(b_1\). Именно он отвечает за направление и угол наклона прямой (и в его формулу входит коэффициент корреляции).
Подтвердить это поможет простой мысленный эксперимент. Представим, что связь между величинами отсутствует (можете воспользоваться сайтом с моделью, чтобы проверить свои предположения). Тогда коэффициент корреляции будет равняться 0, а \(b_0 = \overline{Y}\). И наша прямая пройдет параллельно оси 0Х.
Таким образом мы можем сформулировать статистическую гипотезу для проверки:
И снова мы можем использовать t-критерий, который говорит, что если верна 0 гипотеза, то при многократном выборе нашей выборки с 2 переменными из ГС полученные коэффициенты \(b_1\) распределились бы относительно 0 по t-виду.
Таким образом: \(t = \frac{b_1 - 0}{se(b_1)}\), а число степеней свобод будет \(dF = n-2\) (как и в случае с коэффициентом корреляции). При этом, \(se(b_1) = \sqrt{\frac{1}{n-2} \frac{\sum (y_i - \hat{y_i})^2}{\sum (x_i - \overline{x})^2}}\). Таким образом мы сможем рассчитать вероятность, зная коэффициент \(b_1, se(b_1), dF\).
Примечание. При построении линейных моделей на практике обычно принимается, что переменные взаимосвязаны и зная одну, можно вычислить другую. В таком случае можно не проверять статистические гипотезы. Для этого мы используем сканирующие эксперименты.
Примечание. Приведу разбор формулы для расчета стандартной ошибки наклона (standard error of slope) поскольку найти его оказалось довольно сложно. Чтобы лучше понимать почему формула имеет именно такой вид, нужно ее преобразовать:
Другими словами, стандартная ошибка для коэффициента наклона включает в себя отношение стандартных ошибок поеременных с учетом корня из степеней свободы, с поправкой на степень "объясненного отклонения": \(\sqrt{\frac{SS_{error}}{SS_{total}}}\) (какое количество отклонения от общей дисперсии данных наша модель смогла объяснить).
4.3 Коэффициент детерминации
В предыдущем разделе мы напрямую столкнулись с понятием "объясненной ошибки". Кроме того, мы сталкивались с ним, когда изучали коэффициент корреляции.
Это понятие выражается коэффициентом \(R^2\) - доля дисперсии зависимой переменной (Y), объясняемая регрессионной моделью и формула для его расчета:
где \(SS_{res}\) - сумма квадратов остатков, а \(SS_{total}\) - сумма квадратов общая (расстояние от наблюдения до среднего значения). Можете попробовать математически сравнить эту формулу и формулу для коэффициента корреляции.
По своей сути, коэффициент детерминации определяет отличие получившейся прямой от линии среднего значения (когда верна наша 0-ая гипотеза).
Тогда, если \(R^2 \approx 1\), т.е. \(SS_{total} >> SS_{res}\), то можно сказать, что практически 100% изменчивости нашей зависимой переменной (Y) обусловлены связью с независимой переменной X.
Примечание. Коэффициент детерминации и коэффициент корреляции не взаимосвязаны на логическом уровне. Каждый из них выполняет свою задачу, но в определенных условиях они связаны математически.
Не стоит забывать об ограничениях для применения одномерного регрессионного анализа:
- линейная взаимосвязь X и Y;
- нормальное распределение остатков;
- гомоскадестичность - постоянная изменчивость остатков на всех уровнях независимой переменной. Другими словами - наши отклонения должны быть случайны и не содержать никакой систематической погрешности.
Вот примеры подобных проверок для регрессионной модели. Настоятельно рекомендую изучить все приведенные там случаи и повторить все у себя в RStudio (возьмите код на вооружение для собственных проектов).
Рекомендую поискать различные примеры применение регрессионного анализа и интерпретация результатов , например на курсах в ссылках.
4.4 Заключение
Итак, мы научились строить статистически обоснованную математическую модель и даже оценивать ее достоверность. Но какая же практическая польза от всего этого? Довольно простая - предсказание значений зависимой переменной внутри области работы модели.
Саму модель часто называют линией тренда, что говорит само за себя. И чтобы рассчитать предсказанное значение - нужно просто решить уравнение, при подстановке экспериментально полученного \(x\).
Однако не стоит забывать о существующих ограничениях для линейного регрессионного метода.
- Модель не несет в себе физического смысла и поэтому может выдавать абсолютно некорректные значения при определенных признаках X.
- Линейность системы обычно сохраняется на небольших интервалах и за пределами их часто ведет себя по другому (именно по этому важно перестраивать модель и проводить новые эксперименты - смотри первую часть курса).
- Модель определена только в диапазоне данных, по которым она строилась, и выходить за пределы этих данных крайне опасно.
- Требование к исходным данным, перечисленные ранее.
Развитием рассмотренной линейной регрессии является множественная линейная регрессия, которая позволяет исследовать взаимосвязь одной зависимой и нескольких независимых переменных (как они влияют на нее и какой вклад вносят в модель). По факту - мы уже работали с этими моделями при планировании и анализе факторного эксперимента. На всякий случай освежим в памяти некоторые аспекты множественной регрессии.
- Общий вид уравнения линейной множественной регрессии: \(\hat{y} = b_0 + b_1 x_1 + b_2 x_2 + \dots\).
- Метод наименьших квадратов также позволяет строить модели в n-мерном пространстве признаков. Но теперь остатки - это не расстояние до линии модели, а расстояние до плоскости модели или просто отклонение от n-1 мерной модели.
- Необходимо предварительная проверка на мультиколлинеарность (мы должны использовать только независимые друг от друга признаки, иначе МНК не сможет работать по законам линейной алгебры). Для этого часто оценивают попарную взаимосвязь признаков (рис. 43).
- Прочие требования для одномерной регрессии.
- Для аналитически точных моделей нужно использовать число данных в общем случае в 3 раза больше, чем исследуемых факторов. Если этого не сделать - модель "переобучится", т.е. она слишком хорошо настроится на тестовые данные, но предсказывать реальные данные будет плохо.
- Важно использовать исправленный коэффициент детерминации \(R^2\) (причина аналогична попарному сравнению).
Мы не будем подробно рассматривать данный подход со статистических позиций в настоящем курсе. Если вам интересно разобраться в этой и прочих не освещенных, но упомянутых темах - рекомендую вам изучить курсы, приведенные в списке литературы.
4.5 Вопросы по разделу
-
Если при исследовании взаимосвязи двух переменных коэффициент детерминации оказался равен 0.25 то
- Коэффициент корреляции равен 0.0625
- Коэффициент корреляции равен - 0.5
- Коэффициент корреляции равен 0.5
- Коэффициент корреляции равен 0.5 или -0.5
-
Укажите, на каких графиках значение коэффициента корреляции Пирсона приблизительно равняется нулю.
Рис. q-3. -
Если по результатам исследования мы обнаружили значимую положительную корреляцию уровня преступности и уровня безработицы, то это означает, что:
- Результаты только корреляционного исследования не позволяют нам делать вывод о причинно - следственной связи.
- Безработица - причина преступности.
- Преступность - причина безработицы.
-
Исследователь решил выяснить, существует ли значимая корреляция между словарным запасом школьников и их физическими особенностями. В исследовании приняло участие 11 классов (с 1 по 11 класс, по 30 человек в каждом классе) некоторой школы. Оказалось, что существует значимая положительная корреляция этих двух показателей (r = 0.7, p < 0.05). Исследователь размышляет, какой вывод он может сделать, основываясь на этих данных:
- Доказано влияние роста на словарный запас.
- Доказано влияние словарного запаса на рост.
- Причиной данных результатов, вероятнее всего, является влияние третьей переменной (в каком классе учится школьник), если учесть этот показатель, то значимая взаимосвязь между ростом и словарным запасом не будет обнаружена.
-
Соотнесите графики, на которых изображена регрессионная прямая, и значения коэффициентов \(b_1\) и \(b_0\) в уравнении регрессии: \(\hat{y} = b_{0} + b_{1} \cdot x\). (\(b_1 > 0; b_0 > 0\), \(b_1 > 0; b_0 < 0\), \(b_1 < 0; b_0 > 0\)).
Рис. q-4. -
Укажите верные высказывания:
- Чем больше коэффициент детерминации, тем большая часть дисперсии зависимой переменной обусловлена взаимосвязью с независимой переменной.
- Если коэффициент детерминации равен нулю, то и коэффициент \(b_0\) (intercept) также равен нулю.
- Если коэффициент детерминации равен нулю, то и коэффициент \(b_1\) (slope) также равен нулю.
- Коэффициент детерминации может быть равен единице только в том случае, если корреляция между переменными положительная и равна 1.
-
В случае линейной взаимосвязи двух переменных распределение остатков:
- будет стремиться к нормальному со средним значением, приблизительно равным нулю;
- будет иметь несколько мод;
- будет обладать явно выраженной ассиметрией.
-
Если в нашей модели коэффициент \(b_{1}\) оказался не равен нулю, означает ли это, что обнаружена статистически значимая взаимосвязь (p < 0.05) между исследуемыми переменными?
- Да, коэффициент \(b_1\), не равный нулю, всегда означает, что мы отклоняем нулевую гипотезу
- Нет, коэффициент \(b_1\), не равный нулю, не всегда означает, что мы отклоняем нулевую гипотезу
- Нет, коэффициент \(b_1\) не отвечает за угол наклона регрессионной прямой, его значение никак не влияет на направление взаимосвязи
-
Основываясь на результатах исследования, укажите верные утверждения.
| Estimate | Std. Error | t value | p value | |
|---|---|---|---|---|
| Intercept | 58.70 | 6.452 | 9.100 | 0.000 |
| Age | 1.463 | 0.1023 | 14.30 | 0.000 |
В таблице представлены результаты исследования, посвященного взаимосвязи кровяного давления и возраста у людей в возрасте от 45 до 70 лет. Исследователи применили регрессионный анализ, где в качестве зависимой переменной выступало кровяное давление (pressure), а в качестве независимой переменной - возраст пациентов (age). Согласно полученным результатам, уравнение регрессии будет выглядеть следующим образом:
- Pressure = 58.7 - 1.46*Age
- Pressure = 1.46 - 58.7*Age;
- Pressure = 1.46 + 58.7*Age;
- Pressure = 58.7 + 1.46*Age.
Выберите все подходящие ответы из списка.
- Обнаружена статистически значимая отрицательная взаимосвязь исследуемых переменных.
- С каждым единичным положительным изменением независимой переменной (возраста), ожидаемые значения зависимой переменной (давления) уменьшаются на 58.7.
- Обнаружена статистически значимая положительная взаимосвязь исследуемых переменных.
- С каждым единичным положительным изменением независимой переменной (возраста), ожидаемые значения зависимой переменной (давления) увеличиваются на 1.46.
В данном исследовании коэффициент детерминации оказался равен 0.95. Как мы можем проинтерпретировать этот результат? Укажите все верные высказывания.
- Коэффициент корреляции между нашими переменными близок к 1.
- Коэффициент корреляции между переменными близок к 1 или к -1 (но для однозначного ответа недостаточно данных).
- Коэффициент корреляции между нашими переменными близок к -1.
- Все точки лежат практически на регрессионной прямой.
-
95 % изменчивости зависимой переменной (давление) объясняется нашей моделью.
-
Вообразим мысленный эксперимент. Мы решили исследовать взаимосвязь стоимости (зависимая переменная) и площади квартир (независимая) в городе N. Для этого сформировали выборку из 30 наблюдений и получили, что коэффициент детерминации равен 1 (все наши наблюдения лежат на регрессионной прямой). Означает ли это, что при помощи нашей модели мы можем абсолютно точно предсказывать любые значения стоимости не вошедших в наш анализ квартир, основываясь на их площади?
- Да, коэффициент детерминации, равный единице означает 100 \% по точности прогноз.
- Нет, столь сильная взаимосвязь наших переменных в выборке не означает, что все не включенные в анализ наблюдения также лягут на регрессионную прямую.
- Да, так это означает, что и в генеральной совокупности коэффициент корреляции между стоимостью и площади квартир равен 1.
Литература
- Ресурсы курса Experimentation for Improvement from coursera.org.
- Peter Goos, Bradley Jones. Optimal Design of Experiments. A Case Study Approach.
- Книга к курсу Experimentation for Improvement from coursera.org.
- Tutorial for designing experiments using the R package.
- Изучение R на примере простых инструкций.
- И.А. Реброва. Планирование эксперимента. Омск «СибАДИ» 2010. 107 с..
- Курс "Основы статистики. Часть 1" на stepic.org
- Специализация "Машинное обучение и анализ данных" на coursera.org.
- Курс STAT 503 Design of Experiments. Department of Statistics. PennState Eberly College of Science.
- Неплохая информация по квантилям и как они соотносятся с рангами.
- Неплохое объяснение линейной регрессии с примерами из MS Exel.
- Пост об интерпретации доверительных интервалов..
- Г. Кристиан. Аналитическая химия 1 и 2 том.
- Много полезного материала с неофициального сайта химического факультета МГУ.
- Модели основных экспериментов, разобранных во 2 части.
- К. Дерффель. Статистика в аналитической химии.